Martingale é uma técnica muito popular para apostas em roletas. Ele consiste no seguinte:
-
O jogador aposta uma quantidade monetária pequena em algo com aproximadamente 50% de chance de vencer (par ou ímpar, vermelho ou preto);
-
Caso o jogador vença a aposta, ele aposta a mesma quantidade novamente;
-
Caso o jogador perca a aposta, ele aposta o dobro da quantidade anterior;
-
O jogador continua dobrando a aposta até vencer uma rodada;
-
Retorna à aposta inicial após vencer a rodada.
Uma possível execução deste método é a seguinte:
rodada <- 1:10
aposta <- c(1, 2, 4, 8, 1,
2, 1, 1, 1, 2)
resultado <- c("Perdeu", "Perdeu", "Perdeu", "Venceu", "Perdeu",
"Venceu", "Venceu", "Venceu", "Venceu", "Perdeu")
acumulado <- c(-1, -3, -7, 1, 0,
2, 3, 4, 5, 3)
tabela <- data.frame(rodada, aposta, resultado, acumulado)
kable(tabela, col.names = c("Rodada", "Aposta", "Resultado", "Acumulado"))
| Rodada | Aposta | Resultado | Acumulado |
|---|---|---|---|
| 1 | 1 | Perdeu | -1 |
| 2 | 2 | Perdeu | -3 |
| 3 | 4 | Perdeu | -7 |
| 4 | 8 | Venceu | 1 |
| 5 | 1 | Perdeu | 0 |
| 6 | 2 | Venceu | 2 |
| 7 | 1 | Venceu | 3 |
| 8 | 1 | Venceu | 4 |
| 9 | 1 | Venceu | 5 |
| 10 | 2 | Perdeu | 3 |
Felizmente, é possível automatizar esta tática com uma função no R. Como estou interessado em analisar dados da roleta, sabemos que ela possui 38 números, dos quais 36 podem ser escolhidos pelos jogadores. Desta forma, a probabilidade de vitória é 18/38 caso o jogador aposte em par ou ímpar (ou vermelho ou preto ou algo similar).
martingale <- function(capital_inicial, probabilidade_de_vitoria = 18/38){
capital <- capital_inicial
i <- 2
seq_perdas <- 0
sorteios <- runif(100)
while(tail(capital, 1) > 0){
if (runif(1) < probabilidade_de_vitoria) {
capital[i] <- capital[i-1] + 2^seq_perdas
seq_perdas <- 0
i <- i+1
} else {
capital[i] <- capital[i-1] - 2^seq_perdas
seq_perdas <- seq_perdas + 1
i <- i+1
}
}
return(head(capital, -1))
}
Com isso feito, simulei 1.000 jogos na roleta com as seguintes características:
-
O capital inicial é 10
-
A aposta inicial é 1
-
O jogo para quando a pessoa não puder mais apostar aquilo que o método Martingale exige.
set.seed(1234)
resultado <- data.frame(dinheiro = martingale(10),
tentativa = formatC(1, width = "4", flag = 0))
for (j in 2:1000){
resultado <- rbind(resultado,
data.frame(dinheiro = martingale(10),
tentativa = formatC(j, width = "4", flag = 0)))
}
resultado <-
resultado |>
group_by(tentativa) |>
mutate(x = 1:n(), n = n()) |>
ungroup()
O resultado gráfico das cinco primeiras execuções está abaixo:
library(tidyverse)
theme_set(theme_minimal())
resultado |>
filter(tentativa %in% c("0001", "0002", "0003", "0004", "0005")) |>
ggplot(aes(x = x, y = dinheiro, group = tentativa, colour = tentativa)) +
geom_line() +
scale_colour_viridis_d() +
labs(x = "Quantidade de Rodadas", y = "Dinheiro Acumulado")
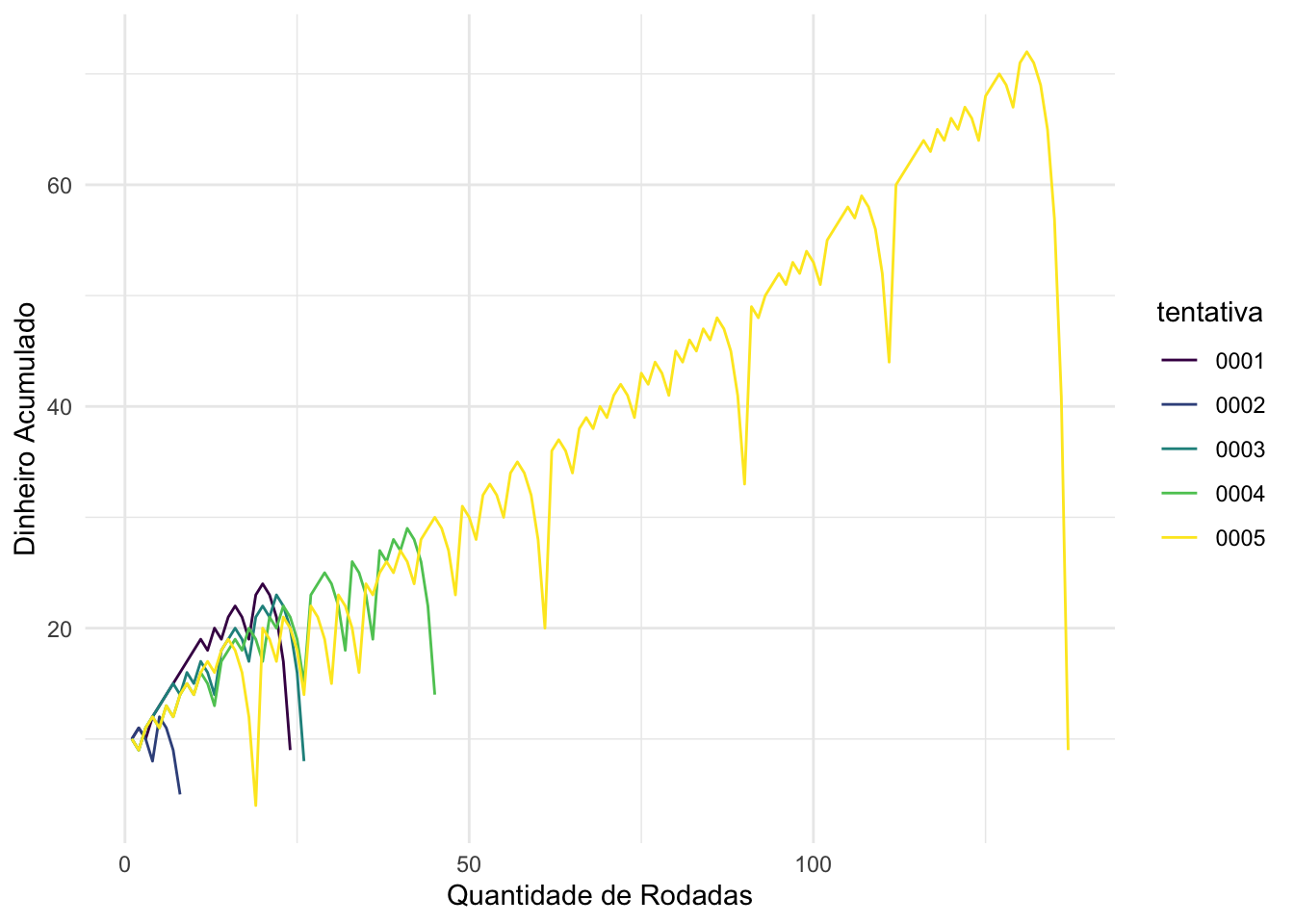
Perceba como os comportamentos gerais dos gráficos são muito similares entre si. O apostador vai jogando e vencendo aos poucos, mas inevitavelmente atinge uma grande sequência de derrotas, fazendo com que ele fique no prejuízo.
É possível medir o número típico de execuções deste método nas condições colocadas na simulação. Para isso, vamos calcular a mediana do número de execuções:
estatistica <-
resultado |>
group_by(tentativa) |>
summarise(tipico = max(n))
estatistica |>
summarise(mediana = median(tipico))
## # A tibble: 1 × 1
## mediana
## <dbl>
## 1 22
Ou seja, metade das simulações realizadas dura até 22 apostas. Ao verificarmos o histograma destes valores, é possível ver que há poucas tentativas realmente longas. Boa parte delas dura muito pouco tempo.
ggplot(estatistica, aes(x = tipico)) +
geom_histogram(binwidth = 100, boundary = 0, closed = "left") +
labs(x = "Número de Jogadas", y = "Frequência")
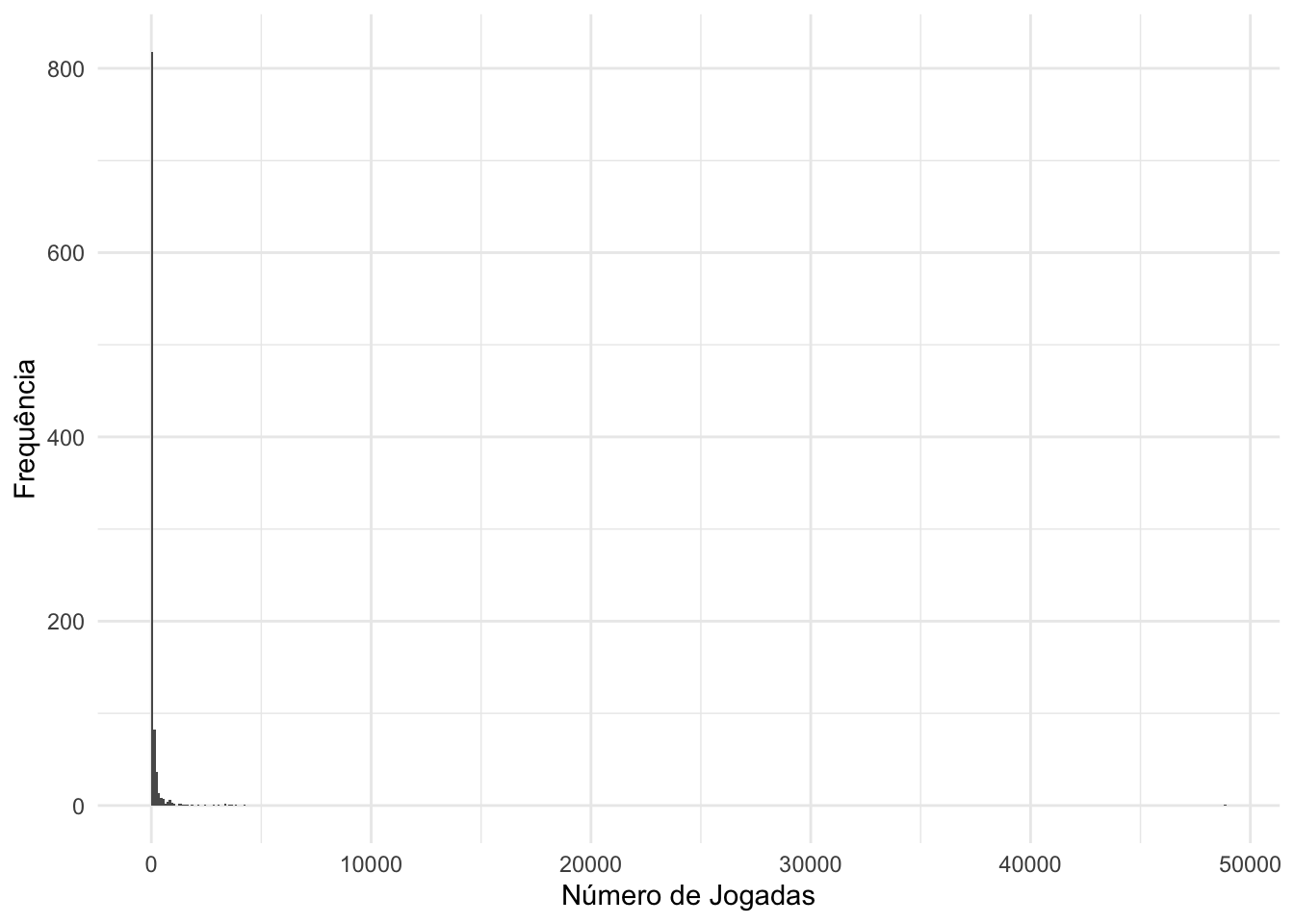
A maior sequência durou 48900 rodadas. Mesmo assim, fica claro que ocorre uma grande sequência de perdas, fazendo com que o lucro obtido caia bastante.
resultado[resultado$dinheiro == max(resultado$dinheiro), ]
## # A tibble: 1 × 4
## dinheiro tentativa x n
## <dbl> <chr> <int> <int>
## 1 23228 0334 48886 48900
resultado |>
filter(tentativa == "0334") |>
ggplot(aes(x = x, y = dinheiro, group = tentativa)) +
geom_line() +
labs(x = "Quantidade de Rodadas", y = "Dinheiro Acumulado")
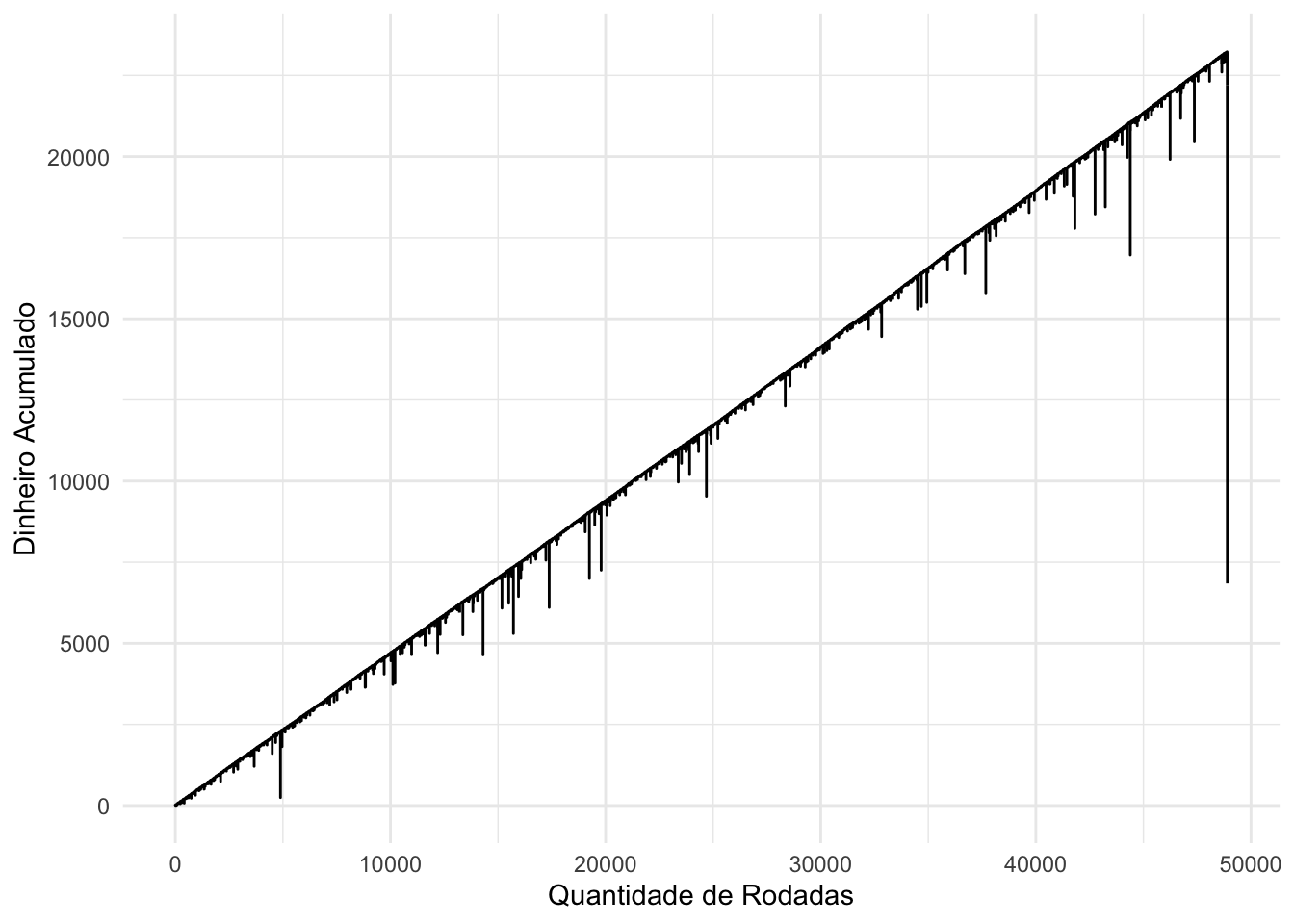
Entretanto, enquanto a média de ganhos fica relativamente grande, a mediana é o valor que melhor representa os resultados obtidos pela população:
resultado |>
group_by(tentativa) |>
summarise(ultimo_valor = tail(dinheiro, 1)) |>
summarise(media = mean(ultimo_valor),
mediana = median(ultimo_valor))
## # A tibble: 1 × 2
## media mediana
## <dbl> <dbl>
## 1 26.7 7
Mais do que isso, 64,4% das pessoas terminaram a simulação com menos do que 10 unidades monetárias, ou seja, ficaram no prejuízo:
resultado |>
group_by(tentativa) |>
summarise(ultimo_valor = tail(dinheiro, 1)) |>
summarise(proporcao = sum(ultimo_valor < 10)/n()*100)
## # A tibble: 1 × 1
## proporcao
## <dbl>
## 1 64.4
Portanto, em resumo, não use martingale para apostar na roleta imaginando que irá ganhar algo no longo prazo. Caso queira apostar, aposte apenas uma quantidade de dinheiro que esteja disposto a perder. Se conseguir lucrar algo a partir disso,