Comparando métodos de imputação de dados no R

Faz um tempo em que gostaria de dar uma olhada no pacote mice do R, para ver como se comportam alguns dos seus métodos ao imputar dados. Para isso, resolvi apagar algumas informações da variável body_mass_g do conjunto de dados palmerpenguins::penguins.

ggplot(penguins, aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point() +
  labs(x = "Comprimento da Nadadeira (mm)", y = "Massa Corporal (g)")

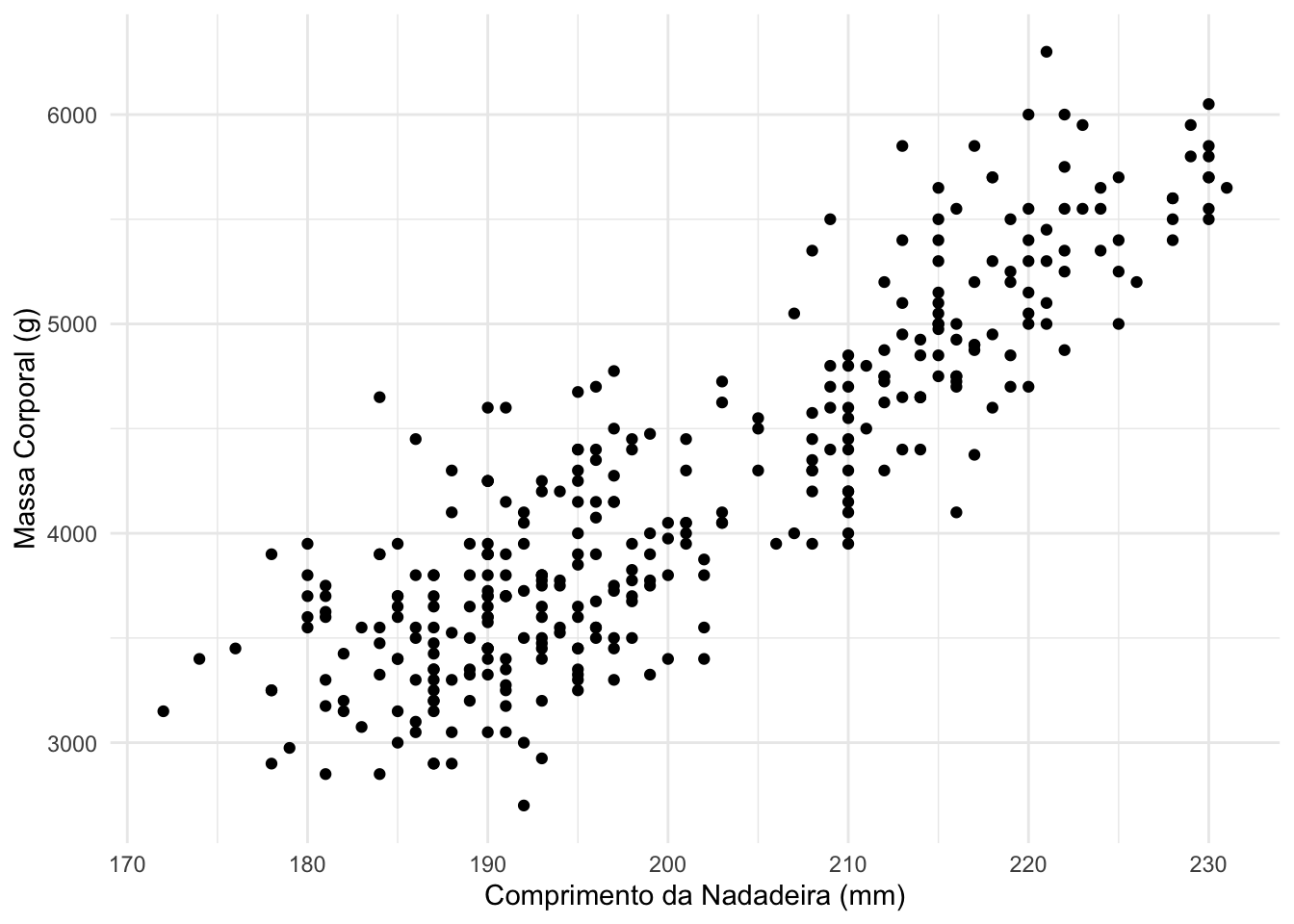
Minnha proposta, neste primeiro teste, é apagar 10% das observações da variável body_mass_g e imputar estes valores utilizando três métodos diferentes. Abaixo apago, de forma aleatória, 10% dos dados deste conjunto.

penguins_missing <- na.omit(penguins)

n <- nrow(penguins_missing)
p <- 0.1

set.seed(1234)

indices <- sample(1:n, n*p)

penguins_missing$body_mass_g[indices] <- NA

Os três métodos que vou comparar são

mean: média incondicional
norm: regressão linear bayesiana
rf: random forest

library(mice)

penguins_missing_media <- complete(mice(penguins_missing, method = "mean"))
penguins_missing_norm  <- complete(mice(penguins_missing, method = "norm"))
penguins_missing_rf    <- complete(mice(penguins_missing, method = "rf"))

Primeiro vou visulizar os resultados de forma gráfica.

bind_rows(mutate(penguins[indices, ], imputacao = "Originais"), 
          mutate(penguins_missing_media[indices, ], imputacao = "Imputados")) |> 
  ggplot(aes(x = flipper_length_mm, y = body_mass_g, colour = imputacao)) +
  geom_point() +
  labs(x = "Comprimento da Nadadeira (mm)", 
       y = "Massa Corporal (g)", 
       colour = "Dados",
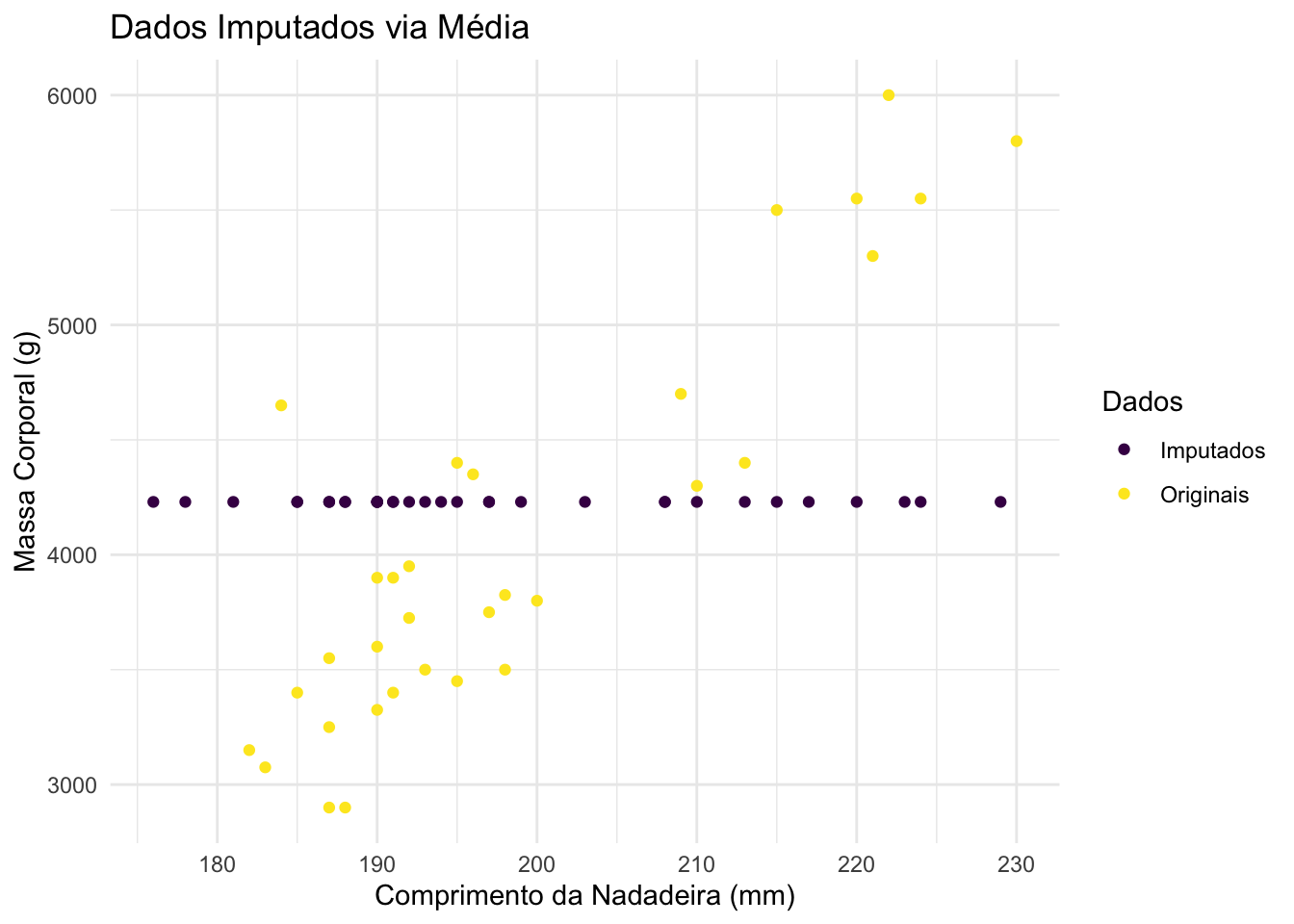
       title = "Dados Imputados via Média") + 
  scale_colour_viridis_d()

bind_rows(mutate(penguins[indices, ], imputacao = "Originais"), 
          mutate(penguins_missing_norm[indices, ], imputacao = "Imputados")) |> 
  ggplot(aes(x = flipper_length_mm, y = body_mass_g, colour = imputacao)) +
  geom_point() +
  labs(x = "Comprimento da Nadadeira (mm)", 
       y = "Massa Corporal (g)", 
       colour = "Dados",
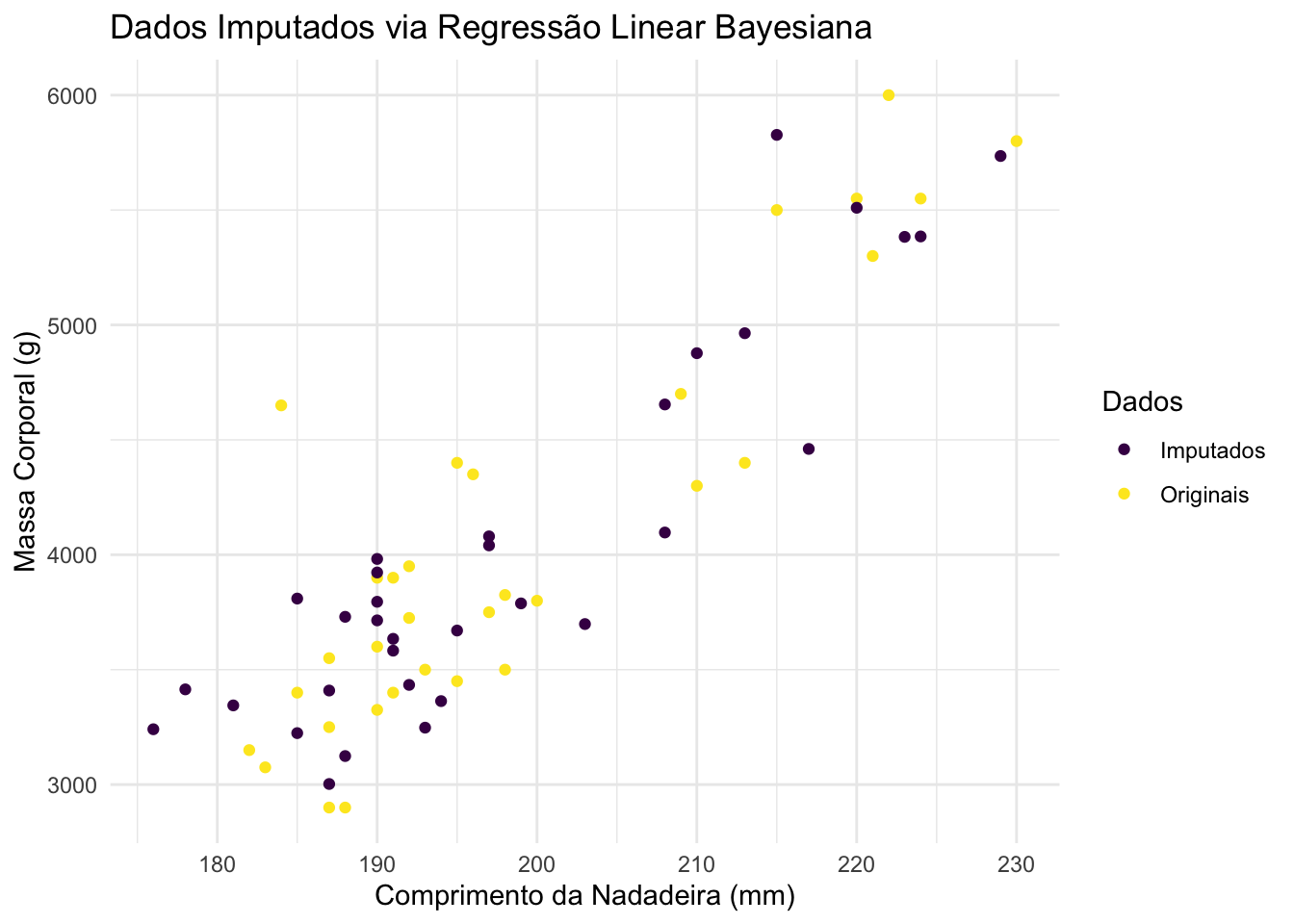
       title = "Dados Imputados via Regressão Linear Bayesiana") + 
  scale_colour_viridis_d()

bind_rows(mutate(penguins[indices, ], imputacao = "Originais"), 
          mutate(penguins_missing_rf[indices, ], imputacao = "Imputados")) |> 
  ggplot(aes(x = flipper_length_mm, y = body_mass_g, colour = imputacao)) +
  geom_point() +
  labs(x = "Comprimento da Nadadeira (mm)", 
       y = "Massa Corporal (g)", 
       colour = "Dados",
       title = "Dados Imputados via Random Forest") + 
  scale_colour_viridis_d()

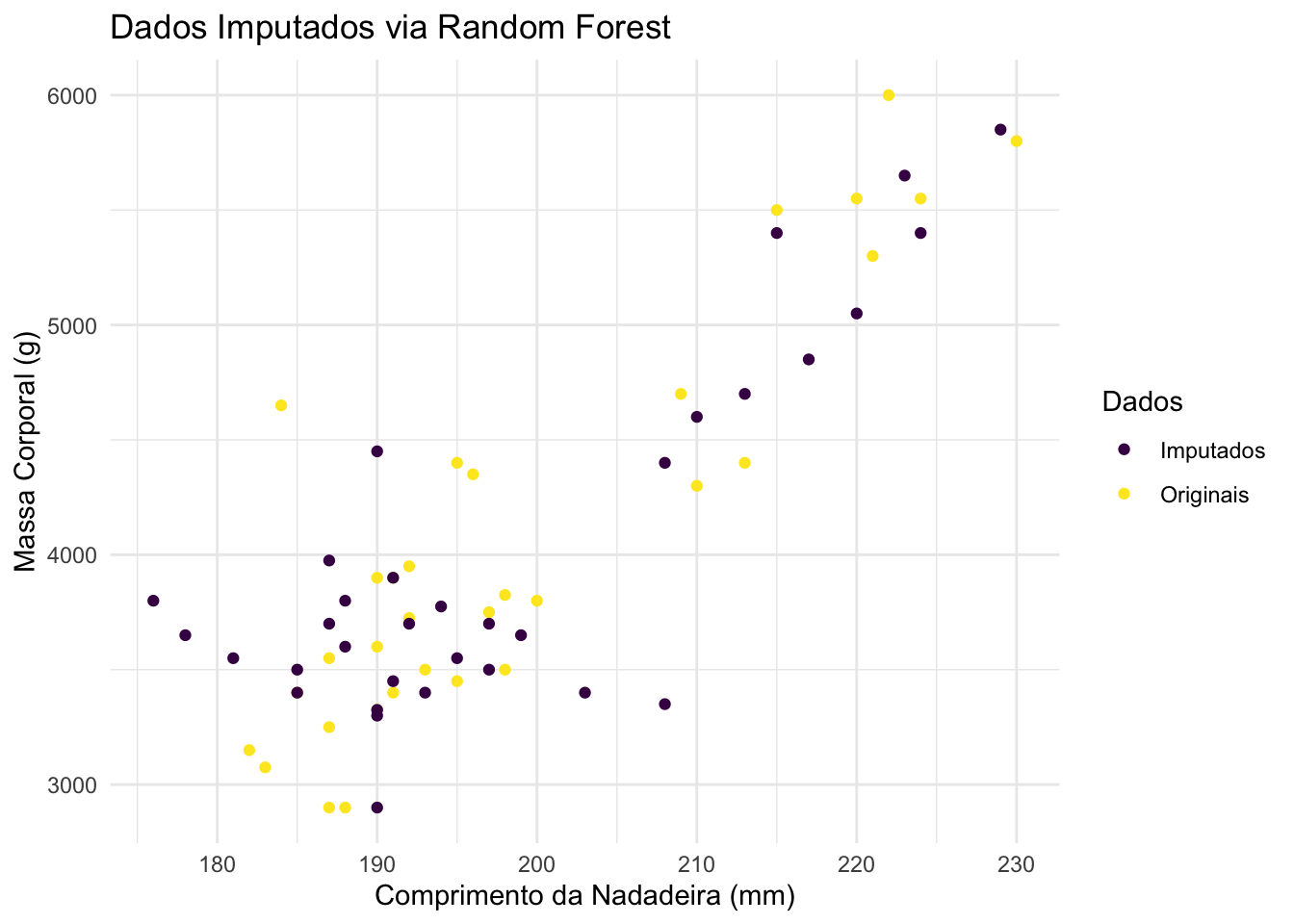
Claramente, a média incondicional levou ao pior resultado. Para decidir entre regressão linear bayesiana e random forest, eu calculo as raízes dos erros quadráticos médios dos métodos de imputação. Desta forma, temos os seguintes resultados:

rmse <- function(x, y){
  sqrt(mean((x-y)^2, na.rm = TRUE))
}

rmse(penguins$body_mass_g[indices], penguins_missing_media$body_mass_g[indices])

## [1] 886.9593

rmse(penguins$body_mass_g[indices], penguins_missing_norm$body_mass_g[indices])

## [1] 693.625

rmse(penguins$body_mass_g[indices], penguins_missing_rf$body_mass_g[indices])

## [1] 757.3468

Portanto, com 693.625, o método de regressão linear bayesiana é o que apresenta o melhor resultado dentre os considerados nesta simulação.