Imagine o seguinte procedimento:
-
Sorteie um número entre 1 e 100
-
Escreva este número por extenso
-
Conte o número de caracteres sem espaço obtidos
-
Represente numericamente este resultado
-
Repita os passos de 2 a 4 até os números começarem a se repetir
Seja, por exemplo, o número 40. Se escrevermos 40 por extenso, temos a palavra quarenta. Se contarmos o número de letras de quarenta, obtemos 8. 8 se escreve oito, que possui 4 caractesres. 4 se escreve como quatro, que possui 6 caracteres. 6 é seis e aí o algoritmo termina.
Se repetirmos isto para todos os números de 1 a 100, obtemos a imagem abaixo:
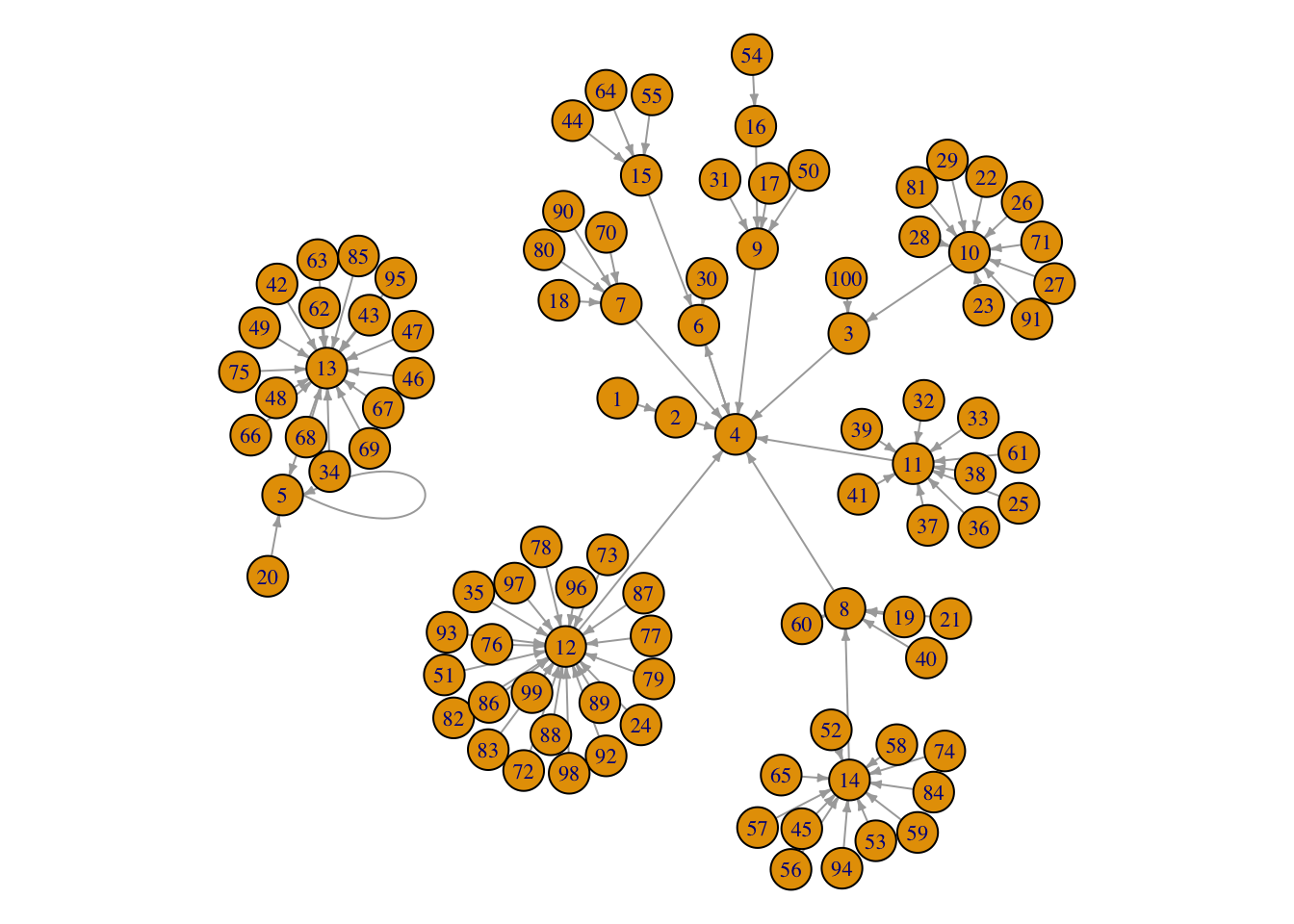
Tente encontrar o número 40 no grafo acima e percorra o caminho descrito no parágrafo anterior.
Perceba que há dois grupos de nomes de números que não conversam entre si. Um dos grupos é formado por aqueles números que ao final do algoritmo ficam alternando entre 6 e 4, como no exemplo acima.
Também há aqueles números que chegam em 5 e por lá ficam.
Também perceba como os números se organizam em torno de alguns valores especiais, como 9, 12, 14, 11, 10 e 13, e partir disso vão para um dos seus destinos finais.
Mas este grafo foi gerado apenas para os números entre 1 e 100. Será que este resultado obtido vale para todos os números? Isto é, se eu tivesse escolhido um valor mais alto, como 4.232.121.935, eu também teria chegado em 4, 6 ou 5 ao repetir este procediento?
Os arquivos utilizados nesta análise podem ser encontrados no github. Pegue-os e tente fazer a sua própria visualização.