O vídeo The Coin Flip Game that Stumped Twitter: Alice HH vs Bob HT propõe uma questão muito interessante. Dois jogadores, chamados Alice e Bob, disputam um jogo. As regras deste jogo são as seguintes:
-
Suponha que uma moeda honesta é lançada 100 vezes em sequência;
-
Alice marca um ponto para cada Cara-Cara (HH) que ocorrer dentro da sequência;
-
Bob marca um ponto para cada Cara-Coroa (HT) que ocorrer dentro da sequência.
A pergunta deste experimento é simples:
Quem tem mais chances de ganhar depois destes 100 lançamentos? Alice ou Bob?
Para ficar claro como ocorre a pontuação do jogo, vamos com um exemplo. Por simplicidade, suponha que a moeda é lançada 5 vezes, com resultado THHHT. Neste caso, Alice marca 2 pontos e Bob 1. Afinal, são quatro sequências de dois lançamentos possíveis em THHHT, destacadas em negrito a seguir:
-
THHHT: ninguém pontua
-
THHHT: Alice pontua
-
THHHT: Alice pontua
-
THHHT: Bob pontua
Portanto, Alice faz dois pontos, enquanto Bob faz um. Desta forma, refaço a pergunta:
Quem tem mais chances de ganhar depois destes 100 lançamentos? Alice ou Bob?
Pense um pouco em sua resposta antes de prosseguir a leitura. Tente justificá-la de forma lógica antes de conferir meus resultados.
Para resolver o problema com 100 lançamentos, eu escrevi um código no R, que simula o lançamento de 100 moedas 10 mil vezes. A função sequência serve justamente para determinar a pontuação de Alice e Bob para cada sequência de lançamento de moedas de tamanho arbitrário.
pontos <- function(sequencia) {
n <- nchar(sequencia)
# crie um vetor com todos os subvetores de tamanho 2
vetor <- substring(sequencia, 1:(n-1), 2:n)
# calcule as quantirades de "HH" e "HT"
alice <- sum(vetor == "HH")
bob <- sum(vetor == "HT")
return(c(alice, bob))
}
Em seguida, testo este código na sequência do exemplo e obtemos o resultado esperado.
sequencia <- "THHHT"
pontos(sequencia)
## [1] 2 1
A partir daqui, rodo a simulação e organizo seus resultados.
repl <- 10000
resultado <- data.frame(alice = NA, bob = NA)
for (j in 1:repl){
sequencia <- paste(sample(c("H", "T"), 100, replace = TRUE), collapse = "")
resultado[j, ] <- pontos(sequencia)
}
Ao visualizá-lo, vemos que é possível, com histogramas, verificar que há diferenças marcantes entre os resultados de Alice e Bob:
resultado |>
pivot_longer(c(alice, bob), names_to = "jogador", values_to = "vitorias") |>
mutate(jogador = ifelse(jogador == "alice", "Alice", "Bob")) |>
ggplot(aes(x = vitorias, fill = jogador)) +
geom_histogram(aes(y = after_stat(density)),
binwidth = 1, position = "identity",
alpha = 0.6) +
labs(x = "Número de Vitórias", y = "Probabilidade", fill = "Jogador") +
scale_fill_viridis_d()
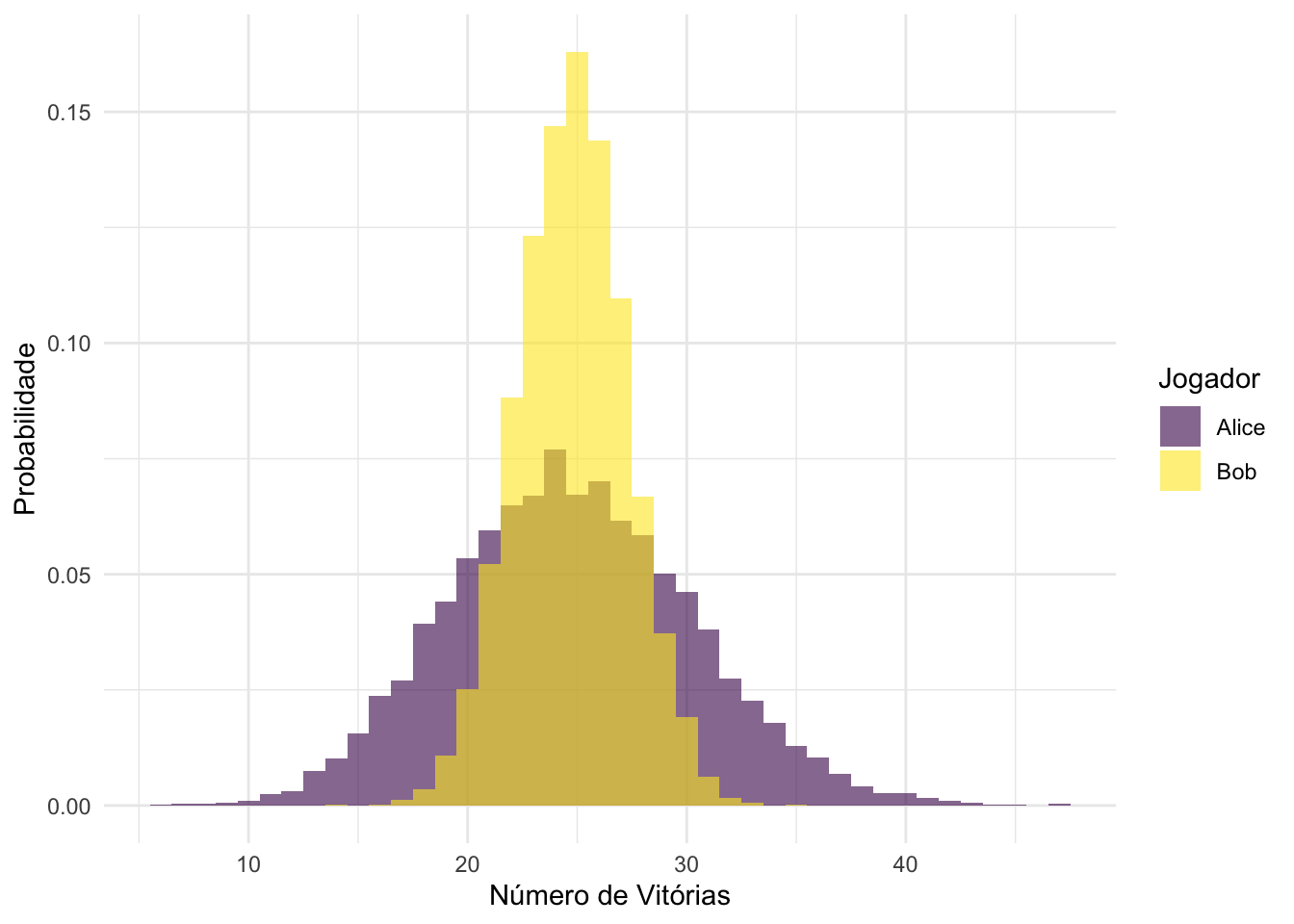
-
Os resultados de Alice possuem uma variabilidade maior;
-
Os resultados de Bob atingem o ponto de máximo em um valor ligeiramente maior do que Alice.
E, de fato, se calcularmos as proporções de vitória de cada jogador, temos a seguinte tabela:
resultado |>
summarise(vitoria_alice = sum(alice > bob) / n()*100,
vitoria_bob = sum(alice < bob) / n()*100,
empate = sum(alice == bob) / n()*100)
## vitoria_alice vitoria_bob empate
## 1 45.78 48.6 5.62
Portanto, é mais vantagem em um jogo como este contar com os resultados HT do que HH.