Após meu post sobre o tempo do cálculo da sequência de Fibonacci no R, resolvi pegar os resultados obtidos no texto e criar uma visualização com eles. Em particular, eu quis ver como o tempo de execução de cada função varia quando os números de Fibonacci crescem. Para isso, eu utilizei as mesmas funções do post anterior:
fibo_recursiva <- function(n){
if (n <= 2){
return(1)
} else {
return(fibo_recursiva(n-1) + fibo_recursiva(n-2))
}
}
fibo_loop <- function(n){
if (n <= 2){
return(1)
} else {
x <- c(1,1)
for (j in 3:n){
x[j] <- x[j-1] + x[j-2]
}
return(tail(x, 1))
}
}
fibo_memoise <- local({
memory <- list()
function(n) {
valueName <- as.character(n)
if (!is.null(memory[[valueName]])) return(memory[[valueName]])
if (n == 0) return(0)
if (n == 1) return(1)
res <- Recall(n - 1) + Recall(n - 2)
memory[[valueName]] <<- res # store results
res
}
})
Em seguida, calculei o tempo de execução de cada função replicada 100 vezes, para cada número de Fibonacci do primeiro ao trigésimo:
library(microbenchmark)
library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ ggplot2 3.5.0 ✔ tibble 3.2.1
## ✔ lubridate 1.9.3 ✔ tidyr 1.3.1
## ✔ purrr 1.0.2
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
theme_set(theme_bw())
j <- 1
resultado <-
microbenchmark(Recursiva = fibo_recursiva(j),
Loop = fibo_loop(j),
Memoise = fibo_memoise(j),
unit = "ms")
resultado <-
tibble(j,
funcao = resultado[[1]],
tempo = resultado[[2]])
for (j in 2:30){
aux <-
microbenchmark(Recursiva = fibo_recursiva(j),
Loop = fibo_loop(j),
Memoise = fibo_memoise(j),
unit = "ms")
resultado <-
resultado |>
bind_rows(tibble(j,
funcao = aux[[1]],
tempo = aux[[2]]))
}
A primeira visualização obtida mostra como o tempo levado pela função recursiva é desproporcionalmente maior do que as funções loop e memoise:
resultado |>
group_by(j, funcao) |>
summarise(media = mean(tempo)) |>
ggplot(aes(x = j, y = media, group = funcao, colour = funcao)) +
geom_point() +
geom_line() +
labs(x = "Número de Fibonacci",
y = "Tempo de Execução Médio em Milissegundos",
colour = "Função") +
scale_colour_viridis_d()
## `summarise()` has grouped output by 'j'. You can override using the `.groups`
## argument.
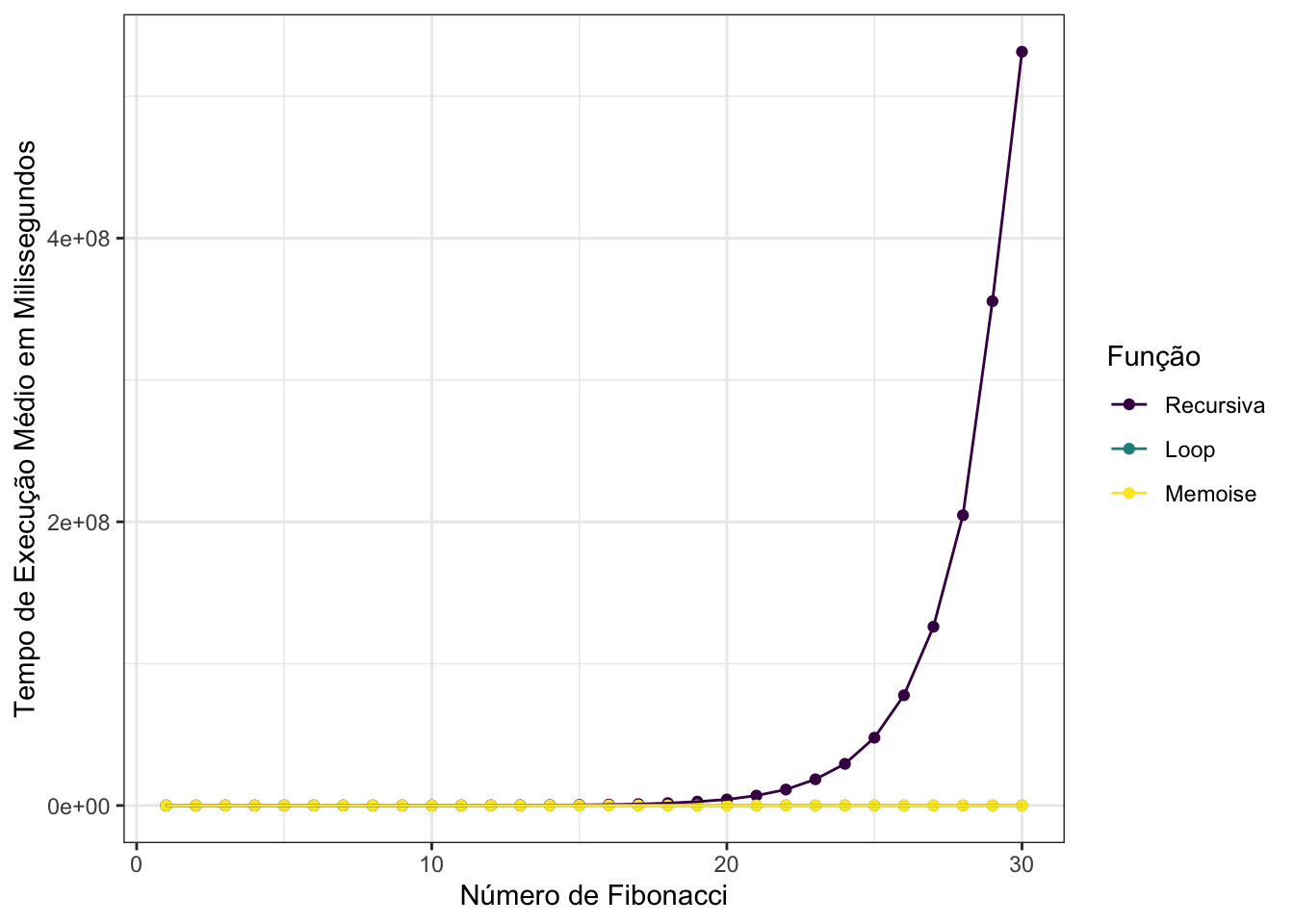
Transformando o eixo y para log10, fica mais fácil de comparar os resultados entre os métodos:
resultado |>
group_by(j, funcao) |>
summarise(media = mean(tempo)) |>
ggplot(aes(x = j, y = media, group = funcao, colour = funcao)) +
geom_point() +
geom_line() +
scale_y_log10(labels = scales::comma) +
labs(x = "Número de Fibonacci",
y = "Tempo de Execução Médio em Milissegundos",
colour = "Função") +
scale_colour_viridis_d()
## `summarise()` has grouped output by 'j'. You can override using the `.groups`
## argument.
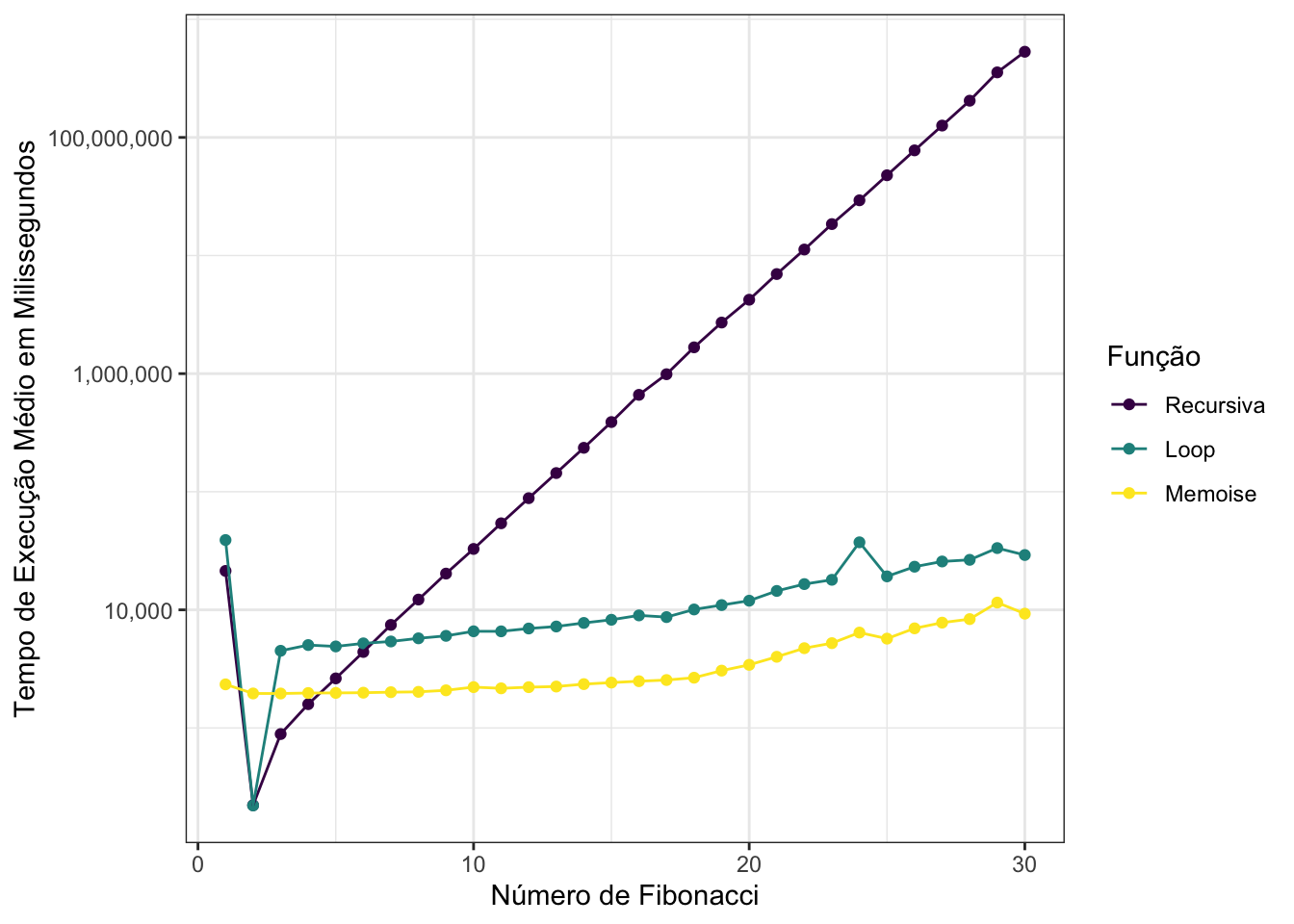
Agora é fácil ver que, exceto pelos primeiro e segundo valores da sequência de Fibonacci, a função Memoise é sempre mais rápida, em média.