Introdução Link para o cabeçalho

Nesse post vou mostrar como faço os gráficos que utilizo para plotar a distribuição normal, seja com ou sem destaques para as suas probabilidades. Na verdade, o método é geral o suficiente para ser facilmente adaptável para qualquer outra distribuição.

Plotando a Curva Normal Link para o cabeçalho

O primeiro passo é plotarmos a curva da distribuição normal. Para isso, vou usar a normal padrão, mas o procedimento é análogo para quaisquer valores de \(\mu\) e \(\sigma\).

library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.1     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

theme_set(theme_bw())

ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101, 
                args = list(mean = 0, sd = 1)) +
  labs(y = "f(x)")

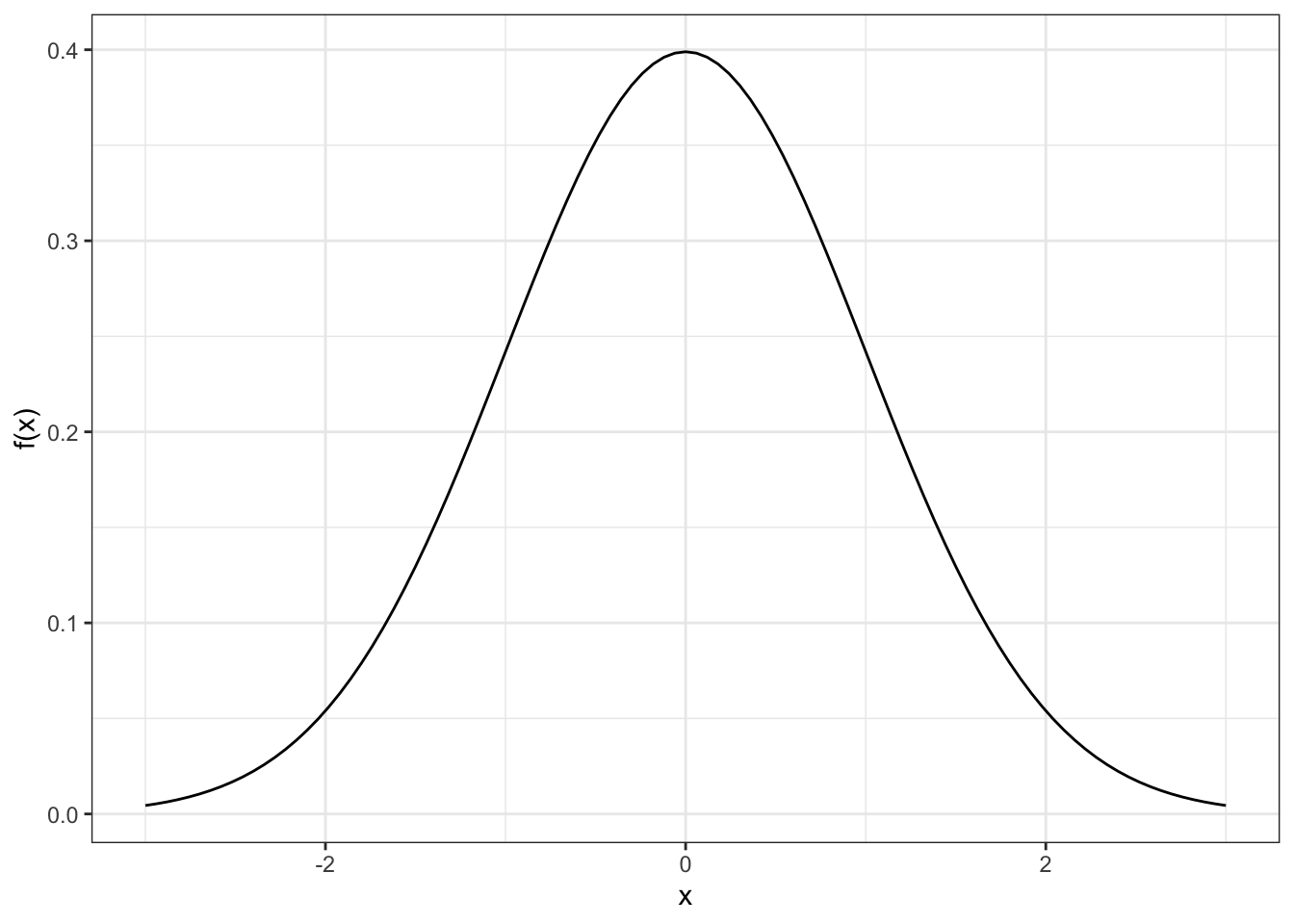
Note que os valores dos limites do data frame criado para o gráfico devem ser adaptados de acordo com a média e o desvio padrão da distribuição desejado. Por exemplo, se \(\mu = 5\) e \(\sigma = 3\), poderíamos fazer o seguinte:

ggplot(data = data.frame(x = c(-4, 14)), aes(x)) +
  stat_function(fun = dnorm, n = 101, 
                args = list(mean = 5, sd = 3)) +
  labs(y = "f(x)")

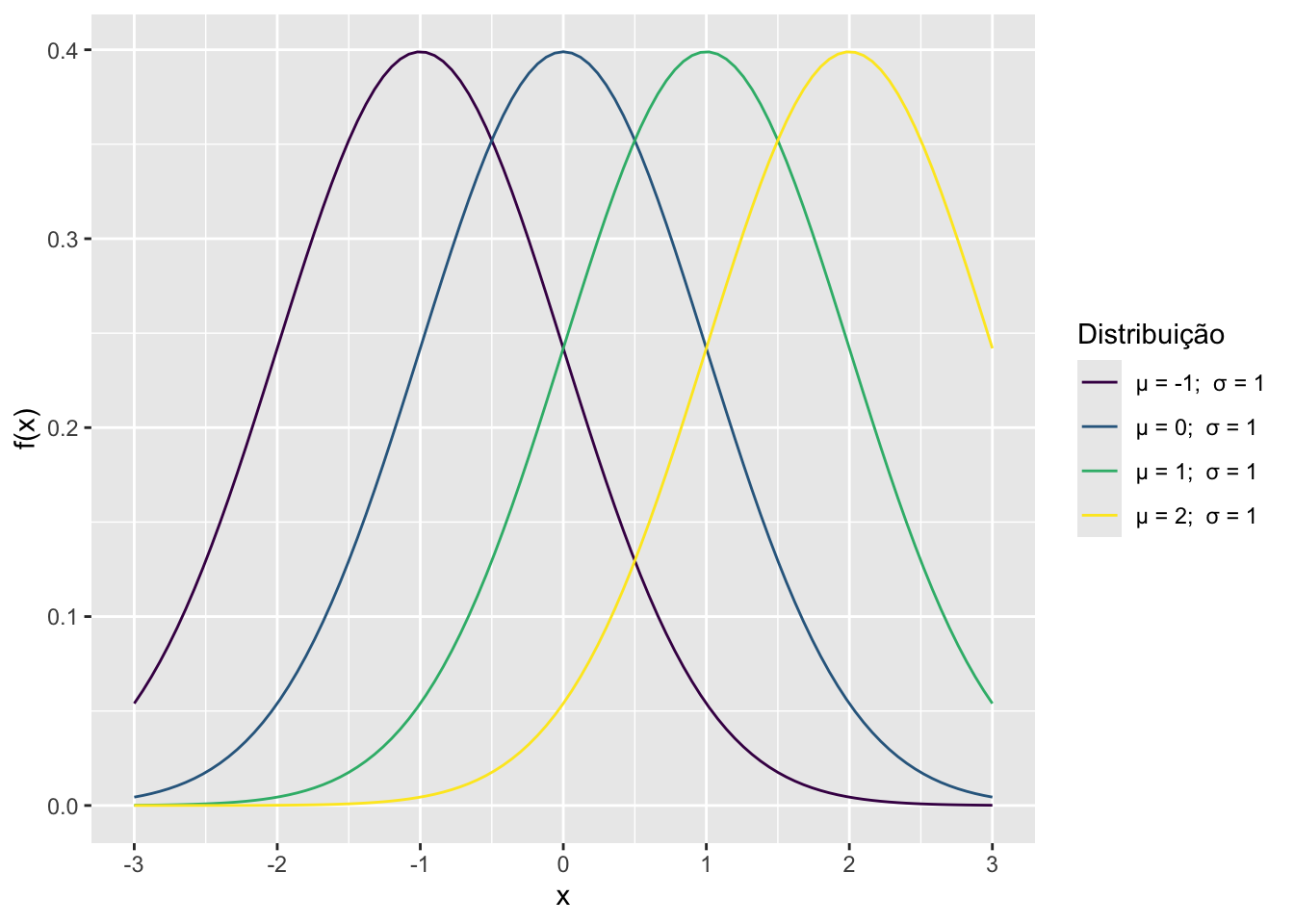
É possível colocar duas ou mais curvas normais plotadas simultaneamente, para compará-las entre si. O procedimento é um pouco mais sofisticado, pois a preparação dos dados é um pouco mais intensa, mas o resultado vale a pena.

# limites e resolucao das curvas a serem criadas

inicio <- -3
fim    <-  3
n      <- 101

x  <- seq(inicio, fim, length.out = n)
y1 <- dnorm(x)
y2 <- dnorm(x, mean = -1)
y3 <- dnorm(x, mean = 1)
y4 <- dnorm(x, mean = 2)

# criacao do conjunto de dados

dados <- data.frame(x, y1, y2, y3, y4)

# dados colocados no formato longo

dados <- 
  dados %>%
  pivot_longer(-x)

# identificacao das distribuicoes

dados$distribuicao <- rep(c(paste("μ", "= 0; ",  "σ", "= 1"),
                            paste("μ", "= -1; ", "σ", "= 1"),
                            paste("μ", "= 1; ",  "σ", "= 1"),
                            paste("μ", "= 2; ",  "σ", "= 1")), 
                          n)

# grafico

ggplot(dados, aes(x = x, y = value, colour = distribuicao)) +
  geom_line() + 
  labs(x = "x", y = "f(x)", colour = "Distribuição") +
  scale_x_continuous(breaks = -3:3) +
  scale_colour_viridis_d()

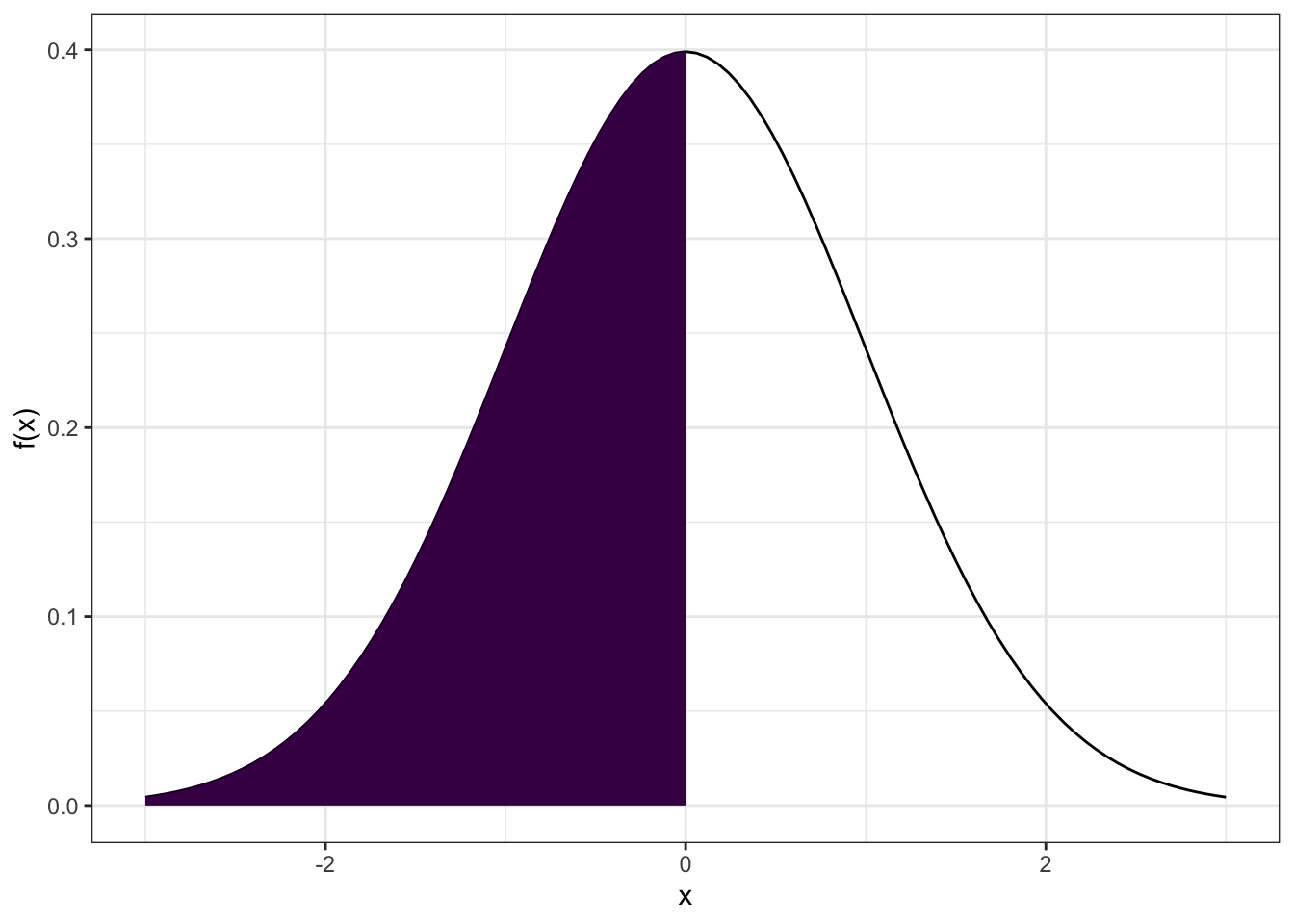
Plotando a Curva Normal com Probabilidades Link para o cabeçalho

Para indicar probabilidades na curva normal é necessário utilizar a função geom_area. De resto, o procedimento permanece bastante parecido. Eu ilustro a aplicação dessa ideia com os três exemplos mais comuns de probabilidades a serem calculadas.

# pacote para definir a cor utilizada

library(viridis)

## Loading required package: viridisLite

# cauda inferior

ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101, 
                args = list(mean = 0, sd = 1)) +
  geom_area(stat = "function", fun = dnorm, fill = viridis(1), xlim = c(-3, 0)) +
  labs(y = "f(x)")

# cauda superior

ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101, 
                args = list(mean = 0, sd = 1)) +
  geom_area(stat = "function", fun = dnorm, fill = viridis(1), xlim = c(0, 3)) +
  labs(y = "f(x)")

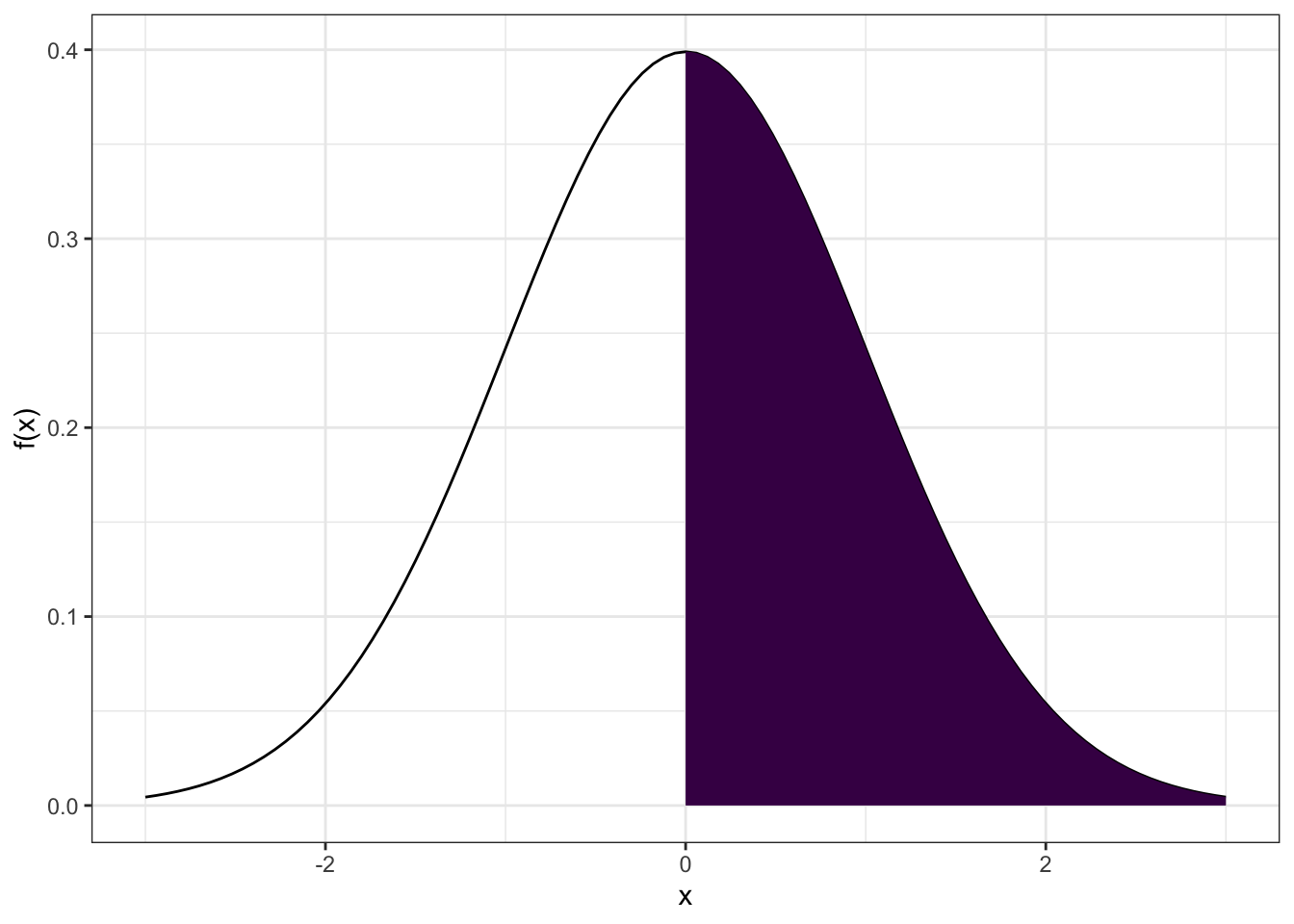
# probabilidade intermediaria

ggplot(data = data.frame(x = c(-3, 3)), aes(x)) +
  stat_function(fun = dnorm, n = 101, 
                args = list(mean = 0, sd = 1)) +
  geom_area(stat = "function", fun = dnorm, fill = viridis(1), xlim = c(-1, 2)) +
  labs(y = "f(x)")

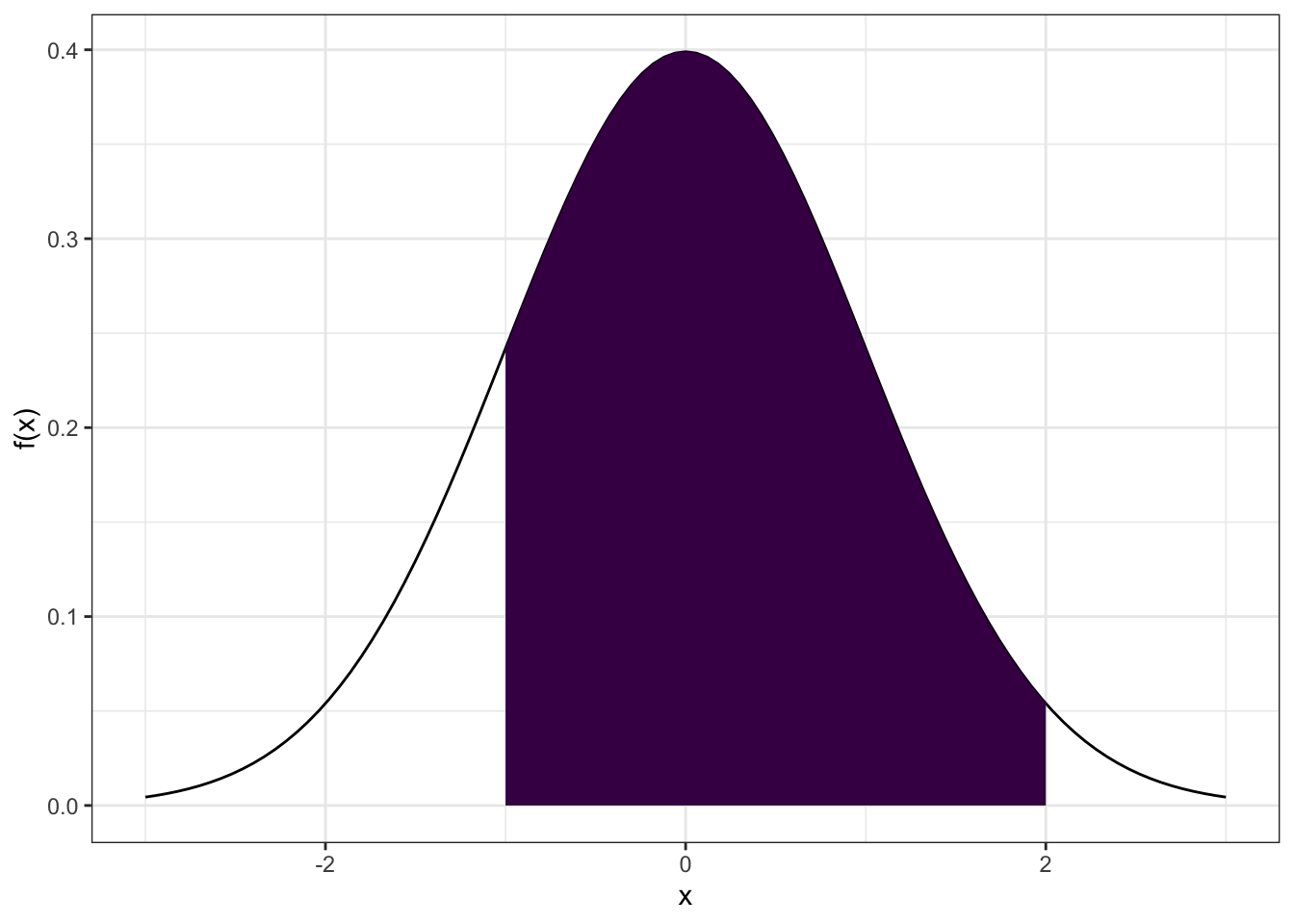
Plotando Outras Distribuições Link para o cabeçalho

O R possui uma grande quantidade de distribuições de probabilidade já implementadas. O site CRAN Task View: Probability Distributions possui uma lista bastante impressionante delas, mas cada usuário pode criar a sua própria função e plotá-la adaptando as instruções deste post.

Abaixo mostro como plotar a densidade das distribuições exponencial e Pareto. Note que é necessário instalar o pacote VGAM para a distribuição de Pareto ser plotada.

# exponencial

ggplot(data = data.frame(x = c(0, 5)), aes(x)) +
  stat_function(fun = dexp, n = 101, 
                args = list(rate = 1)) +
  labs(y = "f(x)")

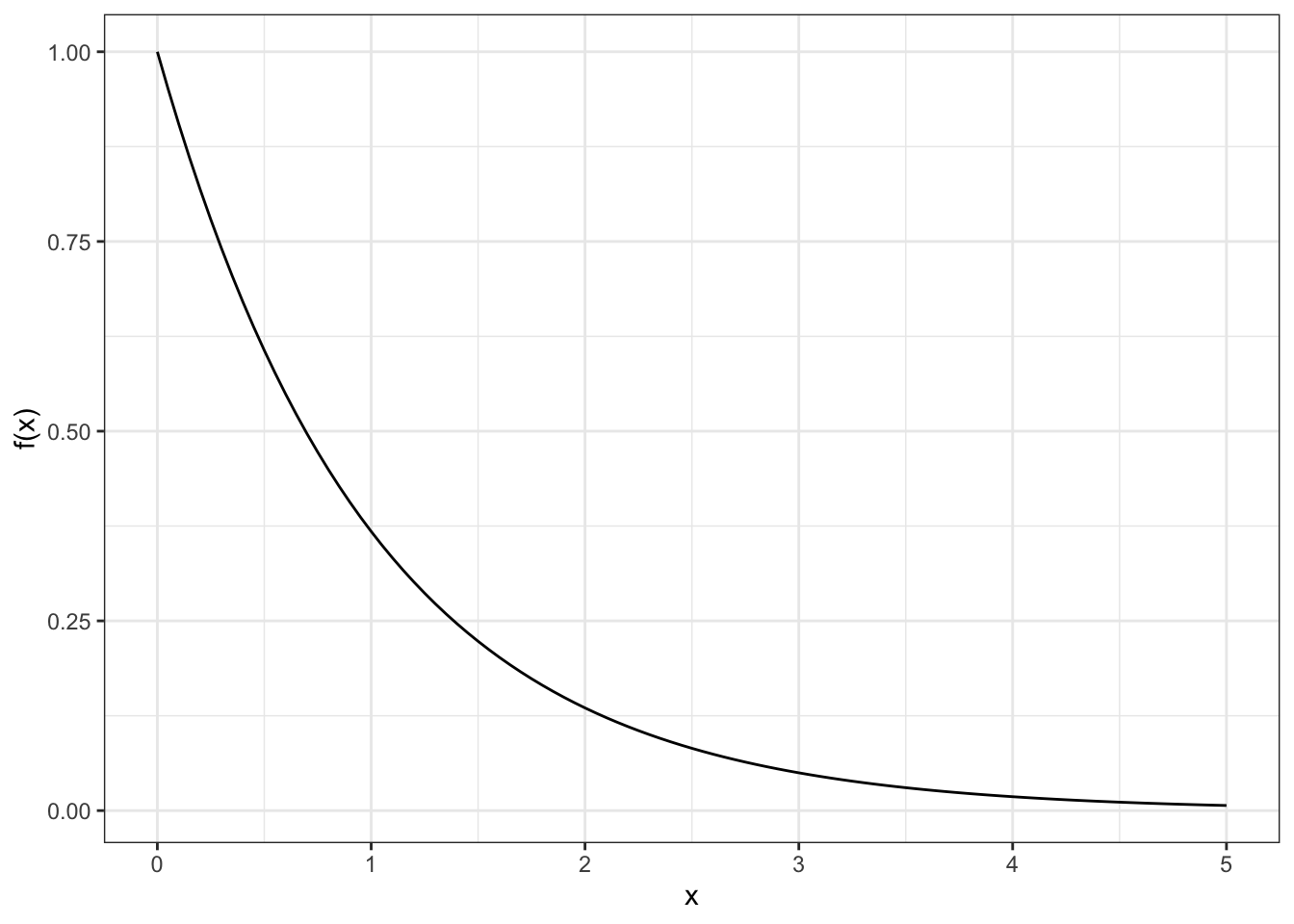
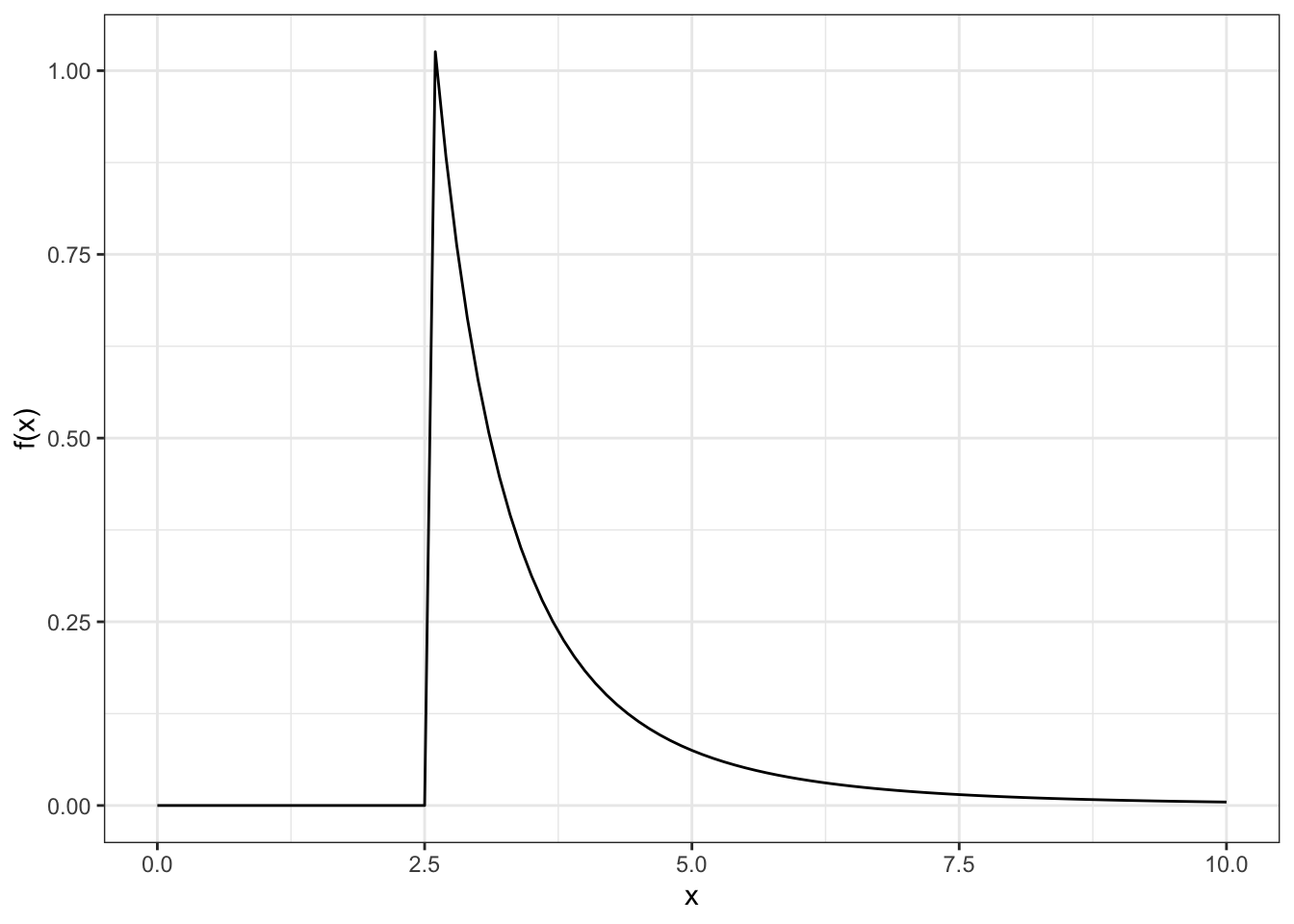
# pareto

library(VGAM)

## Loading required package: stats4

## Loading required package: splines

ggplot(data = data.frame(x = c(0, 10)), aes(x)) +
  stat_function(fun = dparetoI, n = 101, 
                args = list(scale = 2.5, shape = 3)) +
  labs(y = "f(x)")