Encontrei o problema Can You Pass The Cranberry Sauce? na coluna The Riddler, do site FiveThirtyEight. Uma possível tradução para ele é a seguinte:
Para celebrar o Dia de Ação de Graças, você e 19 membros da sua família estão sentados em uma mesa circular (com distanciamento social, é claro^[Foi um problema publicado em 2020, então estávamos em época de pandemia.]). Todos na mesa gostariam de uma porção de molho de cranberry, que por acaso está na sua frente no momento.
Em vez de passar o molho em um círculo, você o passa aleatoriamente para a pessoa sentada diretamente à sua esquerda ou à sua direita. Eles então fazem o mesmo, passando aleatoriamente para a pessoa à sua esquerda ou direita. Isso continua até que todos tenham, em algum momento, recebido o molho de cranberry.
Das 20 pessoas no círculo, quem tem a maior chance de ser o último a receber o molho de cranberry?
Ao conhecer este problema, imaginei que poderia ser resolvido via simulação de Monte Carlo. Minha ideia é simular 100000 vezes o cenário deste jantar e analisar os resultados dos dados produzidos.
Como o problema estava demorando muito tempo para ser resolvido no meu computador, decidi paralelizar o código para otimizar a sua execução. O pacote parallel resolve isso facilmente. Como meu computador possui 8 núcleos, abaixo estou criando um cluster com 7 núcleos, pois deixei um deles livre para outras atividades enquanto o código era executado.
A partir do for, eu começo a simulação na posição 1. A partir disso, vou sorteando a direção para a qual o molho é passado e vou atualizando estas informações. Note que, se por algum motivo a posição se tornar 0, ela automaticamente é transformada em 20. Afinal, as cadeiras estão numeradas de 1 a 20. De modo análogo, se a posição 21 for sorteada, ela automaticamente é transformada em 1. Assim, enquanto cada vetor ordem tiver menos de 20 posições distintas, a simulação é executada.
library(parallel)
clust <- makeCluster(7, type = "PSOCK")
simulacao <- list()
repl <- 100000
for (j in 1:repl){
posicao <- 1
ordem <- 1
i <- 1
while (dim(table(ordem)) < 20){
if (runif(1) < 0.5){
posicao <- posicao - 1
if (posicao == 0){
posicao <- 20
}
} else {
posicao <- posicao + 1
if (posicao == 21){
posicao <- 1
}
}
ordem[i+1] <- posicao
i <- i + 1
}
simulacao[[j]] <- ordem
}
stopCluster(clust)
Agora o objeto simulacao possui 10000 listas, onde cada uma delas corresponde a uma das simulações realizadas. Por isso, cada simulação vai ter um comprimento diferente, pois este comprimento equivale ao número de vezes que o molho foi passado entre os convidados.
A primeira análise que podemos fazer é contar o número de vezes que cada posição na mesa é acessada por último:
resultado <- unlist(lapply(simulacao, tail, 1))
resultado <- as_tibble(resultado) |>
rename(posicao = value)
resultado |>
count(posicao) |>
arrange(desc(n))
## # A tibble: 19 × 2
## posicao n
## <dbl> <int>
## 1 4 5395
## 2 7 5321
## 3 12 5314
## 4 17 5308
## 5 18 5308
## 6 6 5298
## 7 20 5272
## 8 3 5271
## 9 5 5270
## 10 11 5270
## 11 13 5265
## 12 14 5263
## 13 16 5262
## 14 19 5258
## 15 9 5247
## 16 15 5217
## 17 10 5202
## 18 8 5136
## 19 2 5123
Como é possível ver, a posição 20 foi a mais visitada, com 5353 visitas. Por outro lado, a posição 17 foi a menos visitada, com 5133 visitas, indicando uma vantagem de apenas 4,29%. Portanto, note que os valores estão relativamente próximos. Isso pode indicar que eles não são tão diferentes assim. Uma forma de medir isso é através de um gráfico, comparando as probabilidades empíricas de cada posição visitada com a probabilidade teórica de 1/19 de cada posição na mesa ficar por último:
resultado |>
count(posicao) |>
mutate(probabilidade = n/repl) |>
ggplot(aes(x = posicao, y = probabilidade)) +
geom_col() +
geom_abline(slope = 0, intercept = 1/19, linetype = "dashed", colour = "red") +
annotate(geom = "text", x = 3, y = 0.055, label = "1/19") +
scale_x_continuous(breaks = 2:20, minor_breaks = NULL) +
scale_y_continuous(breaks = seq(0, 0.06, 0.01), minor_breaks = NULL, limits = c(0, 0.06)) +
labs(x = "Lugar à mesa", y = "Probabilidade de Ficar por Último")
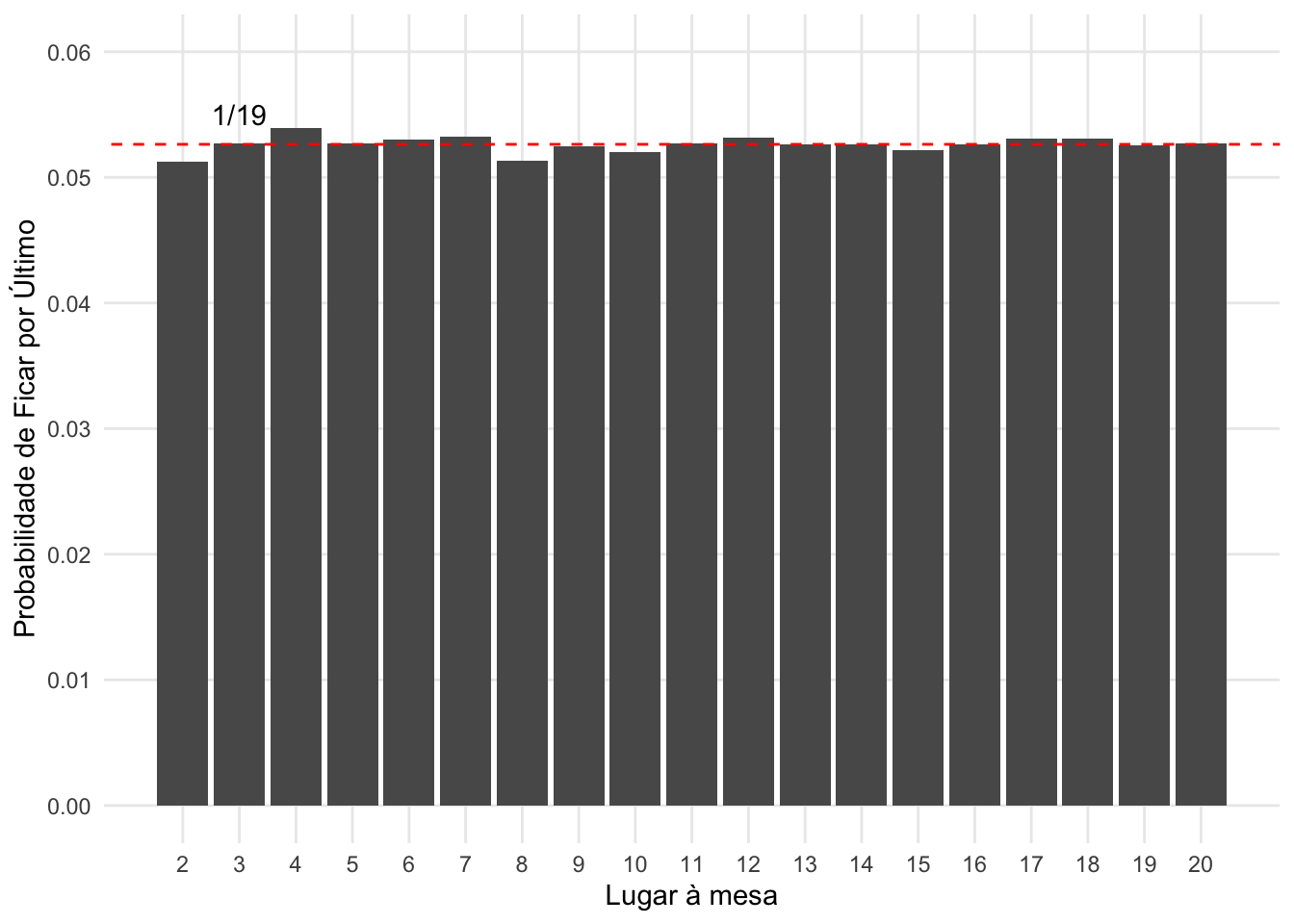
Outra forma seria realizar um teste de qui-quadrado para ver se as probabilidades de cada lugar à mesa são estatisticamente diferentes entre si:
chisq.test(table(resultado))
##
## Chi-squared test for given probabilities
##
## data: table(resultado)
## X-squared = 13.444, df = 18, p-value = 0.7645
Com um p-valor de 0.7645, temos uma certeza muito grande de que estas probabilidades são todas iguais entre si.
Sendo assim, é fácil ver que, surpreendentemente, todas as posições na mesa que não sejam a posição inicial (em meu caso, a posição 1) tem a mesma probabilidade de ficar por último, ou seja, 1/19.
Outra forma de resolver este problema pode ser encontrada em The ‘circular random walk’ puzzle: tidy simulation of stochastic processes in R.