Introdução Link para o cabeçalho
O principal objetivo deste texto é mostrar como é possível, utilizando apenas recursos gratuitos na internet, realizar um projeto de data science do início ao fim. Vamos treinar um algoritmo de classificação de dados baseado em uma técnica chamada Random Forest (link em inglês, pois a Wikipedia em Português ainda não possui um verbete sobre este assunto)], capaz de realizar tanto tarefas de classificação quanto de regressão.
O público-alvo deste texto são as pessoas que já possuem alguma experiência com Estatística e estão interessadas em aprender melhor como aplicar estes conhecimentos já adquiridos em uma área nova, como machine learning. Pessoas com menos experiência talvez tenham um pouco mais de dificuldade na leitura, mas tenho certeza que, ao procederem com calma e atenção, serão recompensados e aprenderão muito.
Preparação do Software Link para o cabeçalho
Quem já possui os programas R e RStudio instalados em seu computador pode pular esta parte do tutorial. Entretanto, sugiro que baixe o arquivo com os códigos organizados para que fique mais fácil de acompanhar este texto.
Há diversos programas disponíveis para fazer data science. Os dois principais são R e python. Este tutorial foi escrito pensado na linguagem R para ser rodado. Particularmente, prefiro o R ao python, pois a sintaxe dele é, para mim, mais fácil de entender. Mas isto é gosto pessoal. Tudo o que foi feito aqui pode ser adaptado e realizado em qualquer outra linguagem que o leitor prefira, como python, julia ou matlab, por exemplo.
Se o seu computador não possua o R e o RStudio instalado, clique nos links abaixo e instale-os.
-
R: este programa é o cerne da análise. É ele que vai realizar os cálculos e plotar os gráficos da análise.
-
RStudio: a interface padrão do R não é muito amigável de utilizar. Entretanto, é possível melhorá-la para que ela fique mais interativa. Desta forma, nossa produtividade aumenta. Portanto, o RStudio serve para melhorar a utilização do R, deixando-a mais dinâmica.
Uma característica do R é que suas funções podem ser expandidas com comandos e funções criados pela comunidade. E são milhares (se não forem milhões) de expansões assim. Estas expansões estão em pacotes que podem ser instalados via internet. Para instalar os pacotes extras necessários para esta análise, abra o RStudio e vá ao menu File > New File > R Script, como mostra a figura abaixo:
Com o script aberto, rode o comando abaixo e aguarde. Vários arquivos serão baixados e o R vai informando o progresso da instalação.
install.packages(c("tidyverse", "corrplot", "GGally", "caret", "rpart", "rpart.plot"), dependencies = TRUE)
Este passo pode demorar um pouco, dependendo da velocidade da sua conexão com a internet.
Com tudo preparado, é hora de começar a análise.
Análise Exploratória dos Dados Link para o cabeçalho
Como não poderia deixar de ser, a primeira parte de um projeto de data science segue a mesma lógica de um projeto de análise estatística de dados. Precisamos fazer a análise exploratória a fim de entender o conjunto de dados com o qual estamos trabalhando.
O conjunto de dados que vou baixar se chama Iris Flower Dataset. Por ser multivariado e com um número razoável de observações, este conjunto é bastante famoso na literatura estatística. Até mesmo Fisher já trabalhou conceitos de análise multivariada com estes dados.
Seu nome é Iris porque foram coletadas observações de 150 sujeitos de 3 espécies de flores do gênero Iris: Iris setosa, Iris versicolor e Iris virginica. Mais informações sobre estas flores podem ser encontradas na Wikipedia.
Embora o conjunto de dados iris esteja disponível em qualquer instalação do R, este tutorial vai mostrar como obter dados diretamente da internet. Então é isto que faremos abaixo, baixando este conjunto iris diretamente do site do UCI Machine Learning Repository e processando-o na sequência para análise.
# definir o endereco do conjunto de dados e baixa-lo
url <- "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
iris <- read.csv(url, header = FALSE)
names(iris) <- c("c_sepala", "l_sepala", "c_petala", "l_petala", "especie")
# remover a string 'Iris-' do inicio de cada tipo de especie
iris$especie <- as.factor(gsub("Iris-", "", iris$especie))
# estatistica descritiva basica
summary(iris)
Com isso, percebemos que temos um conjunto de dados formado por cinco variáveis. Quatro destas variáveis são quantitativas e uma é categórica. As variáveis são
-
c_sepala: comprimento da sépala das flores
-
l_sepala: largura da sépala das flores
-
c_petala: comprimento da pétala das flores
-
l_petala: largura da pétala das flores
-
especie: espécie da flor
Há diversas atividades que podem ser feitas com este conjunto de dados. O que farei aqui é uma tarefa de classificação. Vou ajustar um modelo que vai prever a espécie da planta baseado nas quatro dimensões de cada uma delas.
É importante qual o objetivo do nosso primeiro projeto de data science logo no seu começo. Assim, podemos direcionar nossas análises diretamente para este fim, sem perder tempo realizando atividades que não contribuem para o nosso objetivo.
Com o objetivo definido, vamos fazer algumas análises básicas. A primeira delas é verificar se existe correlação entre as nossas variáveis. Perceba que vou retirar a coluna 5 desta análise porque ela não é uma variável quantitativa.
library(corrplot)
correlacao <- cor(iris[, -5])
corrplot.mixed(correlacao, upper = "ellipse")
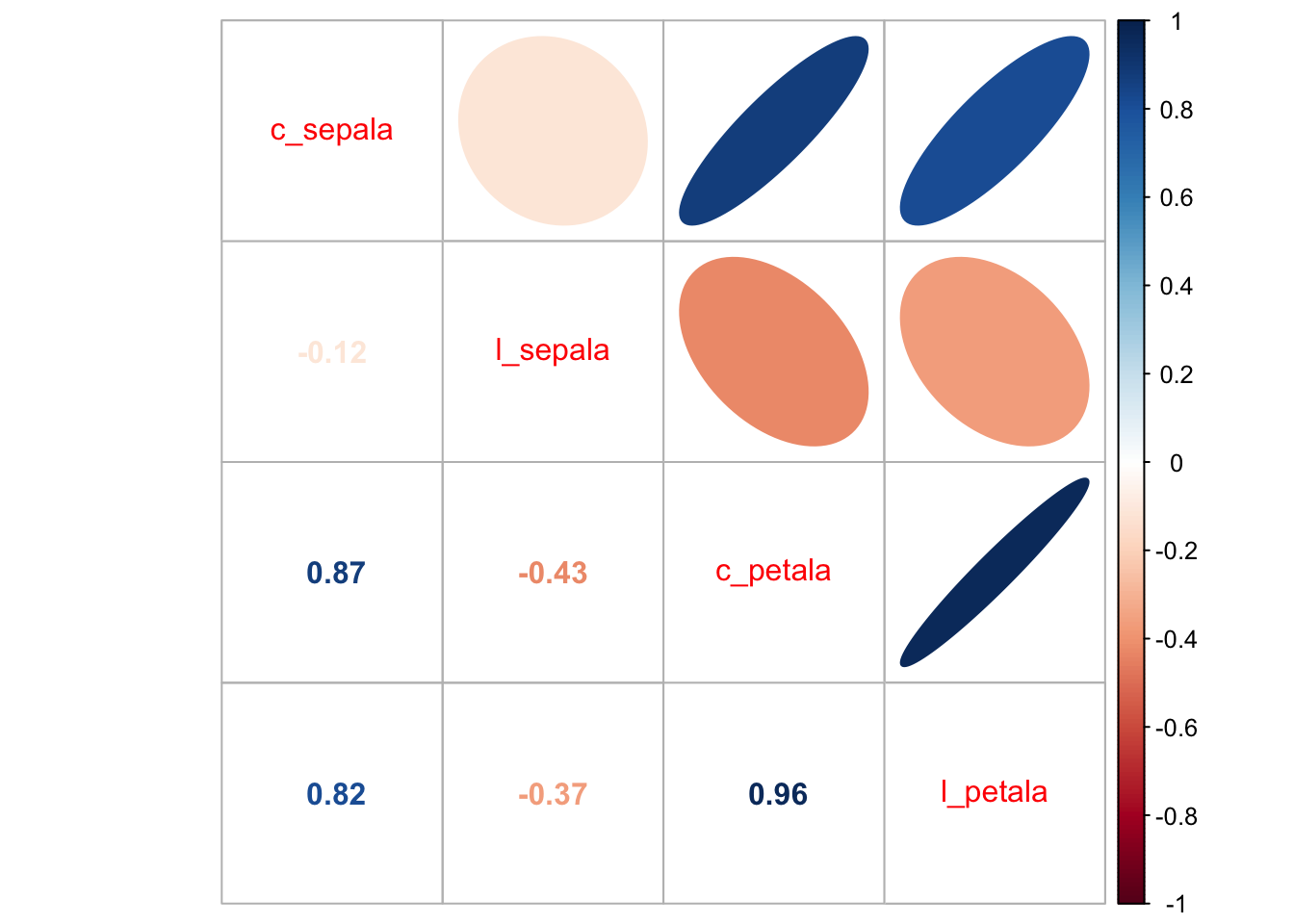
Podemos perceber que existem valores razoáveis de correlação entre algumas das combinações de variáveis. Em particular, entre o comprimento e a largura da pétala. Podemos visualizar isto em um gráfico de dispersão:
library(tidyverse)
theme_set(theme_bw())
ggplot(iris, aes(x = c_petala, y = l_petala)) +
geom_point()
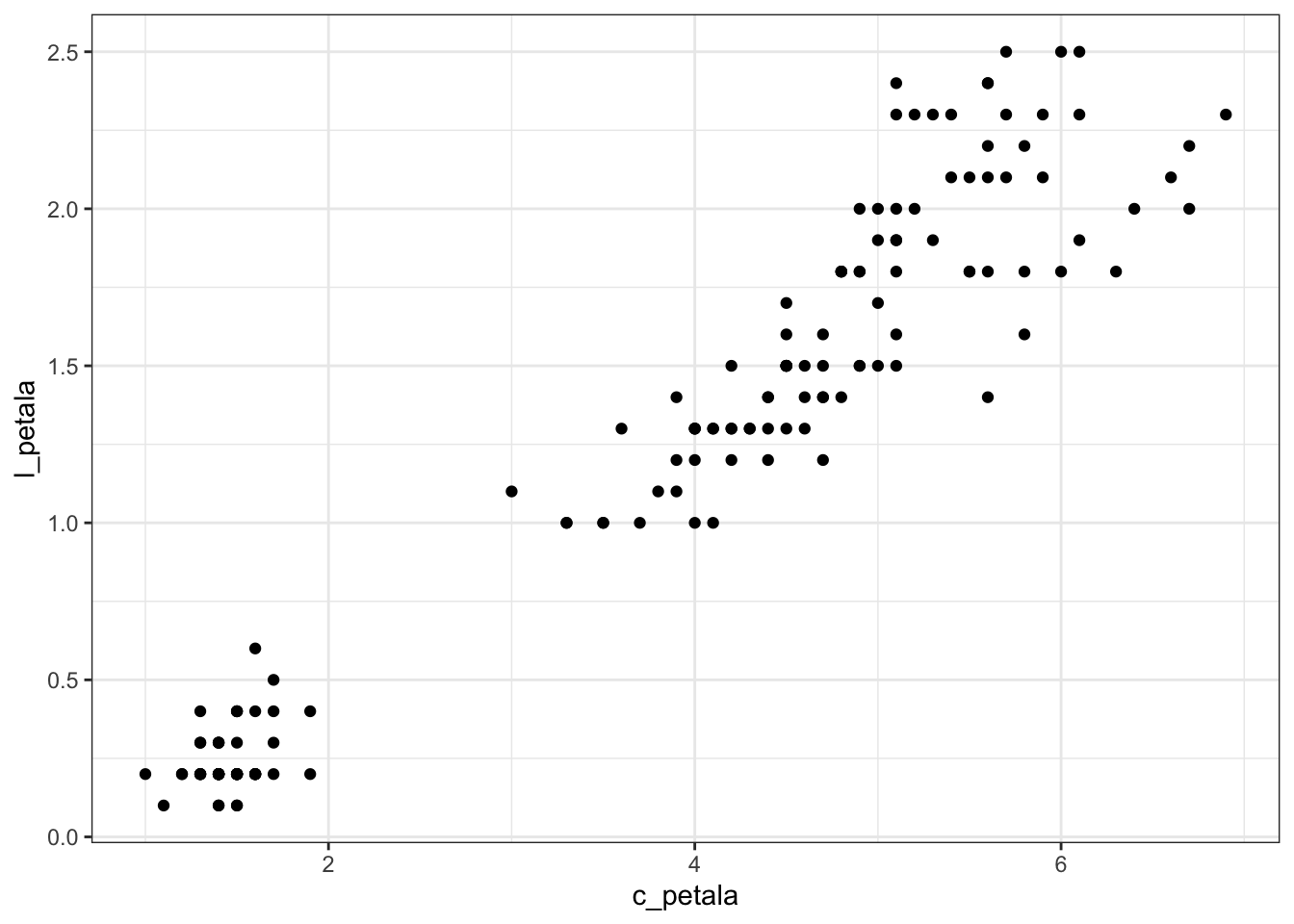
Embora já vejamos a relação que existe entre as variáveis comprimento e largura da pétala, podemos colocar mais informações neste gráfico. Por exemplo, podemos colorir os pontos de acordo com a espécie da planta.
ggplot(iris, aes(x = c_petala, y = l_petala, colour = especie)) +
geom_point()
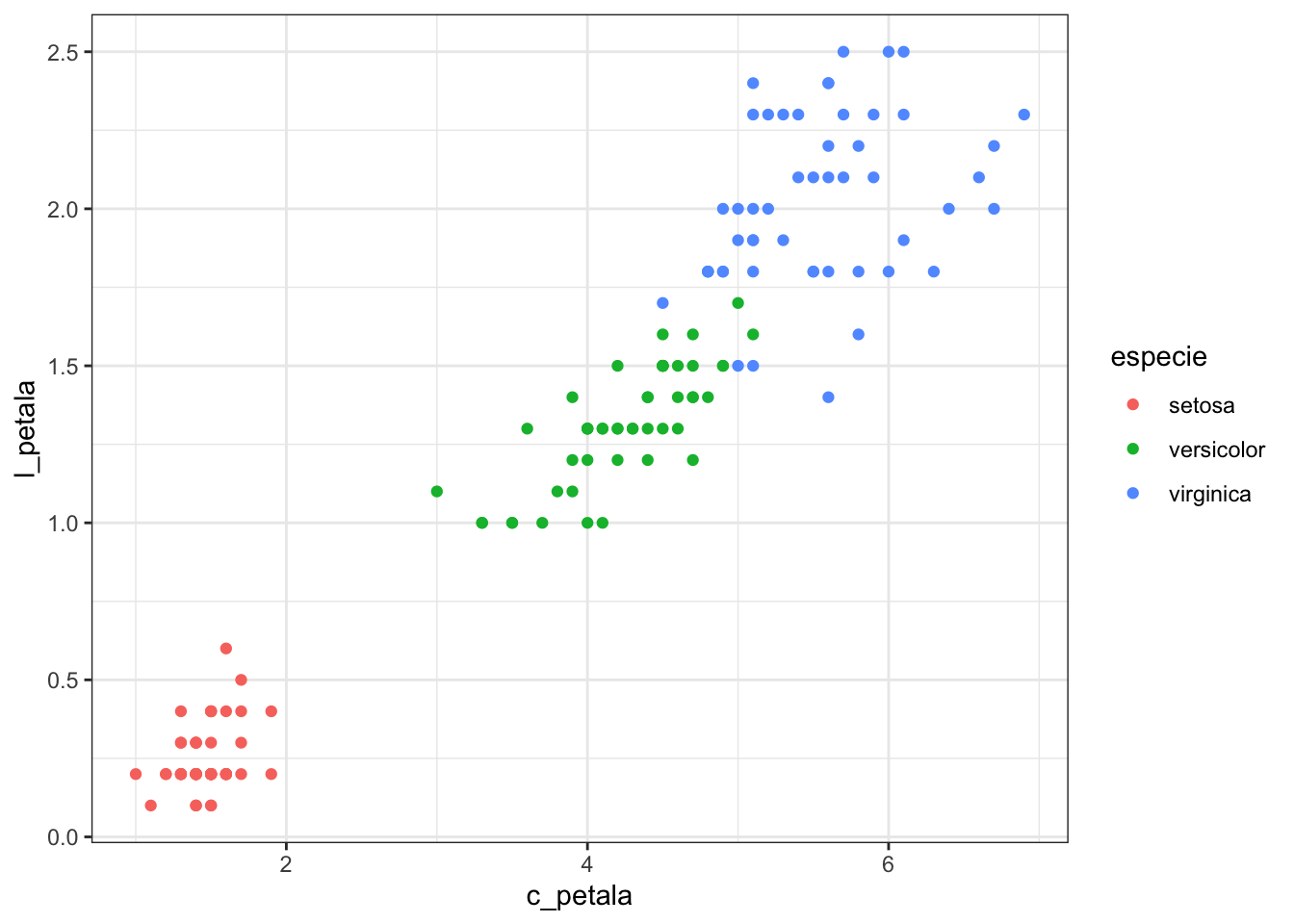
Agora podemos ver que o grupo de flores da espécie setosa está bastante separado dos demais. Esta é uma informação importante, pois queremos construir um algoritmo de classificação de espécies. Por outro lado, perceba que as espécies versicolor e virginica estão quase se confundindo uma com a outra. Isto pode acabar prejudicando um pouco o desempenho do nosso algoritmo de classificação.
A fim de verificar como é o comportamento das outras variáveis, podemos extender o gráfico anterior para todas a combinações de variáveis neste conjunto de dados. Em vez de repetirmos manualmente o código, vamos utilizar a função ggpairs do pacote GGally:
library(GGally)
# remover a variavel especie, pois nao eh quantitativa
ggpairs(iris[, -5], aes(colour = iris$especie))
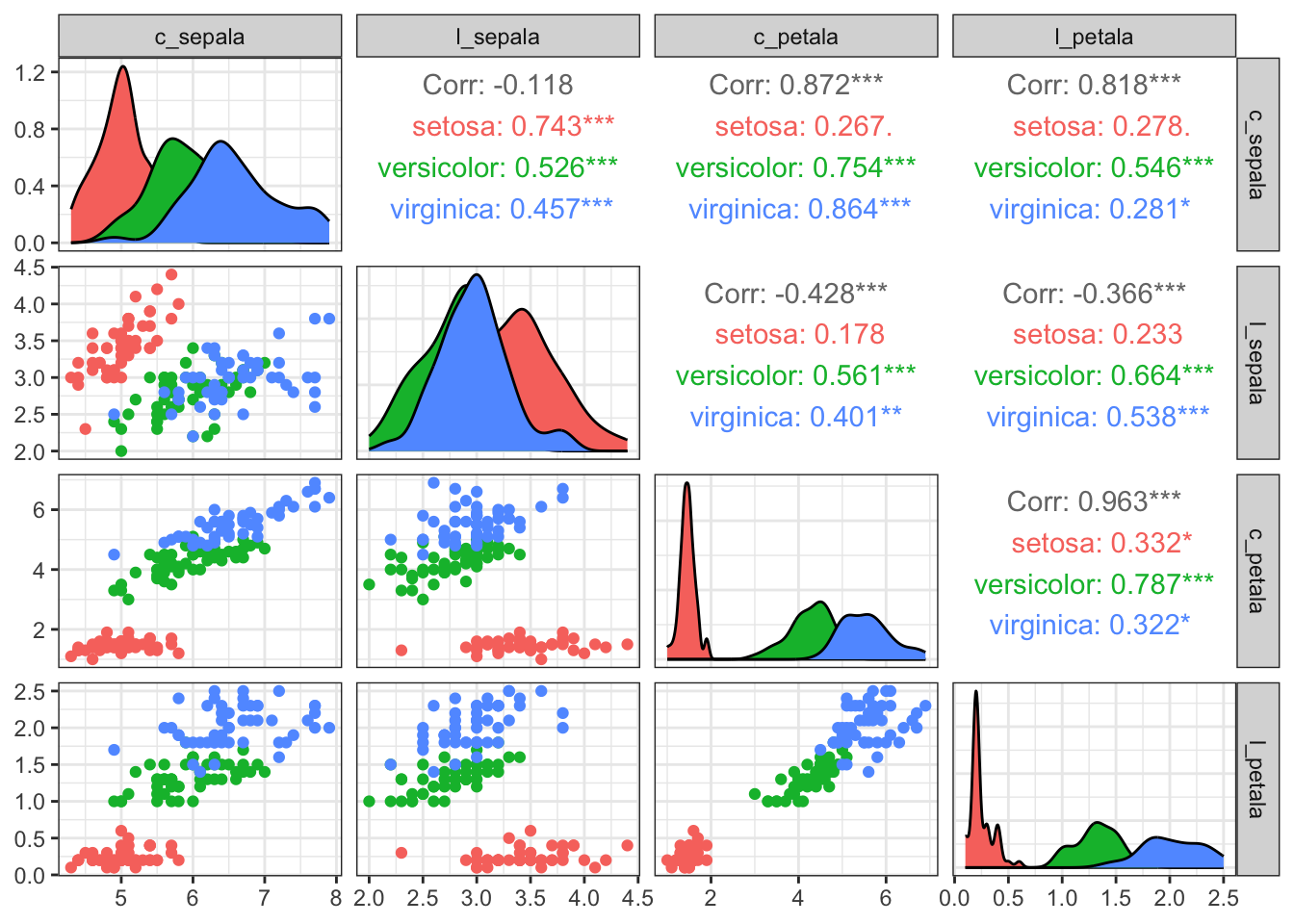
Veja que agora temos muitas informações sobre nossos dados. Para quem já tem alguma experiência em análise de dados, o que vemos é o seguinte:
-
Diagonal principal: estimativas da função densidade de cada uma das quatro variáveis, de acordo com a espécie de flor
-
Triângulo inferior: gráficos de dispersão das variáveis do conjunto de dados, duas a duas
-
Triângulo superior: correlação total entre as variáveis e correlação dentro de cada grupo
Com a análise exploratória dos dados terminada, podemos partir para o ajuste do modelo.
Ajuste do Modelo Link para o cabeçalho
Há uma infinidade de opções quando falamos de ajuste de modelos de classificação. Neste tutorial vou utilizar o Random Forest, que é poderoso o suficiente, além de ter convergência rápida e ser de fácil utilização.
O Random Forest é baseado em árvores de classificação. Sem entrar muito fundo na parte teórica, uma árvore de classificação é um modelo matemático que utiliza a estrutura de árvore de decisão para classificar dados. Melhor do que explicar isto em palavras é ver o algoritmo em ação:
library(rpart)
library(rpart.plot)
modelo <- rpart(especie ~ ., method = "class", data = iris)
prp(modelo, extra = 1)
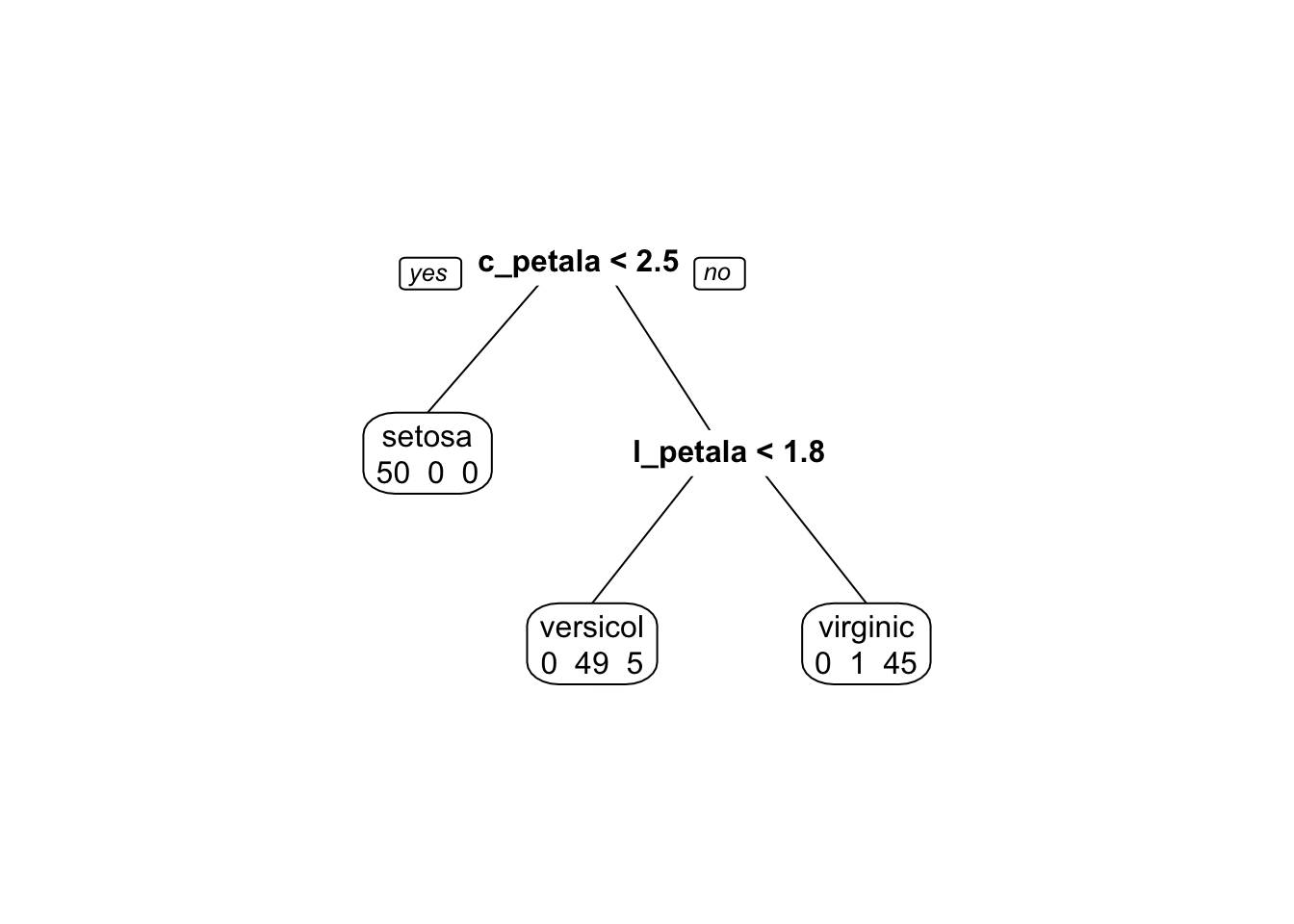
Perceba que é feita uma pergunta em cada nó da árvore. A resposta da pergunta determina se outra pergunta será feita ou se a árvore chegou ao fim e a classificação foi terminada. Além disso, o erro de classificação é determinado ao final da árvore.
Uma Random Forest (ou Floresta Aleatória) é a combinação de centenas de árvores de classificação. Este resultado segue do fato de que a combinação de diversos modelos diferentes é melhor do que um modelo sozinho.
Conjuntos de Treino e Teste Link para o cabeçalho
Um problema que surge no ajuste de modelos de classificação e regressão é o sobreajuste. O sobreajuste ocorre quando o modelo se ajusta muito bem aos dados, se tornando ineficaz para prever observações novas.
O gráfico abaixo ilustra este conceito no contexto de um modelo de classificação.
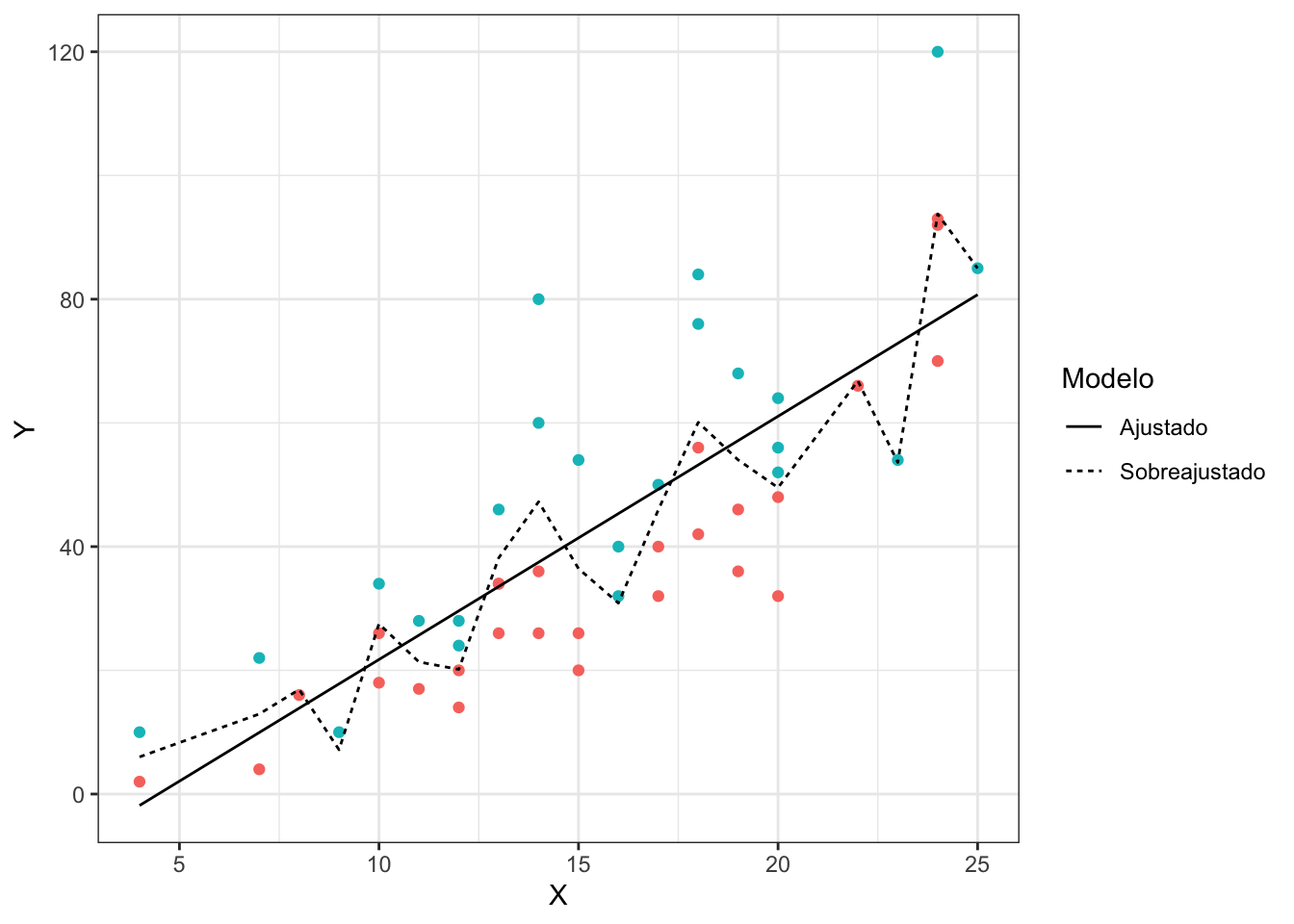
Note como o modelo sobreajustado acompanha os dados muito mais de perto, enquanto o modelo ajustado segue a tendência geral de separação dos pontos. A desvantagem de ter um modelo que acompanhe os dados de maneira muito próxima é a perda de generalidade. Este tipo de modelo funciona muito bem para um conjunto de dados específico, mas vai se comportar muito mal se novas observações forem coletadas.
Uma forma de evitar este problema é dividindo aleatoriamente o conjunto de dados original em duas partes mutuamente exclusivas. Uma destas partes é chamada de conjunto de treino e, a outra, conjunto de teste. A ideia por trás disso é ajustar o modelo aos dados de treinamento e simular a entrada de novas observações através do conjunto de teste. Assim, é possível verificar quão bem ou quão mal o modelo ajustado está se comportando ao prever observações que não foram utilizadas em seu ajuste.
Para fazer isto no R utilizamos a função createDataPartition do pacote caret.
library(caret)
# definir 75% dos dados para treino, 25% para teste
trainIndex <- createDataPartition(iris$especie, p = 0.75, list = FALSE)
iris_treino <- iris[ trainIndex, ]
iris_teste <- iris[-trainIndex, ]
Ao fazer iris_treino <- iris[ trainIndex, ] eu estou dizendo que o conjunto de dados iris_treino vai ter as linhas de iris com os números presentes em trainIndex. De modo análogo, iris_teste <- iris[-trainIndex, ] diz que o conjunto de dados iris_teste não vai ter as linhas de iris com os números presentes em trainIndex
Agora tenho dois data frames novos em minha área de trabalho. 75% das observações estão no conjunto de treino e 25% no conjunto de teste. Esta divisão é arbitrária. Normalmente, recomenda-se que o conjunto de treino tenha de 70% a 80% das observações. O restante das observações irá fazer parte do conjunto de teste.
Ocorre que esta divisão dos dados em dois grupos tem uma desvantagem. Isto acaba fazendo com que tenhamos menos dados para ajustar o modelo. E, com menos dados para ajustar o modelo, menos informação temos. Com menos informação, pior ficará nosso modelo. Uma maneira de reduzir este efeito é através da validação cruzada.
Validação Cruzada Link para o cabeçalho
A validação cruzada é mais um método utilizado para evitar sobreajuste no modelo. A ideia é ajustar diversas vezes o mesmo modelo em partições (conjuntos mutuamente exclusivos) do conjunto de treinamento original. Neste exemplo eu vou utilizar um método chamado validação cruzada \(k\)-fold.
Esta técnica consiste em cinco passos:
-
Separar o conjunto de treinamento em
\(k\)folds (ou partições) -
Ajustar o modelo em
\(k-1\)folds -
Testar o modelo no fold restante
-
Repetir os passos 2 e 3 até que todos os folds tenham sido utilizados para teste
-
Calcular a acurácia do modelo
Entretanto, precisamos definir o número de folds a serem utilizados na validação cruzada. Em geral, a literatura sugere que de 5 a 10 folds sejam usados. O desempenho dos algoritmos não melhora de maneira considerável se aumentarmos muito o número de folds.
Dependendo do tamanho do conjunto de dados, é possível que muitos folds acabem deixando-nos sem observações para os conjuntos de teste dentro da validação cruzada. Por este motivo, é sempre bom controlar este parâmetro de acordo com o conjunto de dados que estamos estudando.
Com estas técnicas definidas, podemos finalmente passar para o ajuste do modelo.
Ajuste do Modelo Link para o cabeçalho
Como dito anteriormente, vamos ajustar um modelo chamado Random Forest aos dados das flores. Para realizar este ajuste precisamos criar os conjuntos de treino e teste e fazer a validação cruzada do modelo a ser ajustado. Como já criamos os conjuntos de treino e teste anteriormente, apenas precisamos nos preocupar com a validação cruzada do modelo.
Felizmente, o pacote caret já possui o algoritmo da validação cruzada implementado. Só precisamos ser explícitos no ajuste do modelo para que este método seja utilizado.
O caret utiliza duas funções para ajustar modelos aos dados, chamadas train e trainControl. Basicamente, a função trainControl estabelece os parâmetros utilizados no ajuste do modelo. Abaixo estou exemplificando como definir que desejamos fazer validação cruzada com 5 folds.
fitControl <- trainControl(method = "cv",
number = 5)
Com os parâmetros da validação cruzada definidos, podemos partir para a o ajuste em si.
ajuste_iris <- train(especie ~ .,
data = iris_treino,
method = "rf",
importance = TRUE,
trControl = fitControl)
Note que defino várias coisas com a função train:
-
especie ~ .é a notação de fórmula do R, aquele mesma que se utiliza para se ajustar modelos de regressão linear com a funçãolm. Neste exemplo eu estou dizendo que quero preverespecieem função de todas as outras variáveis do conjunto de dados. -
data = iris_treinoinforma para o R em qual conjunto de dados ele deve procurar as variáveis presentes na fórmula definida acima -
method = "rf"diz que vou ajustar um modelo do tipo Random Forest. Uma grande vantagem de usar o pacotecareté poder aprender uma sintaxe apenas e poder ajustar centenas de algoritmos diferentes, apenas mudando o argumentomethodda funçãotrain. -
importance = TRUEé um argumento opcional que nos permitirá, posteriormente, fazer seleção de variáveis -
trControl = fitControldefine as opções da validação cruzada
Para saber o resultado do ajuste, basta chamar o objeto ajuste_iris:
ajuste_iris
## Random Forest
##
## 114 samples
## 4 predictor
## 3 classes: 'setosa', 'versicolor', 'virginica'
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 92, 90, 91, 91, 92
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 2 0.9738801 0.9607672
## 3 0.9829710 0.9744318
## 4 0.9829710 0.9744318
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 3.
Note que há um parâmetro chamado mtry no output acima. Este parâmetro significa que os modelos foram ajustados com 2, 3 e 4 variáveis preditoras selecionadas aleatoriamente (na verdade, quando mtry = 4 temos todas as variáveis preditoras utilizadas no modelo). Ao final, o melhor modelo é aquele que utiliza 2 variáveis preditoras.
Este resultado pode variar dependendo de como os dados foram selecionados durante as criação do conjunto de treinamento e teste e também de como a validação cruzada foi realizada, principalmente se estivermos com conjuntos de dados pequenos como este que utilizamos neste projeto.
Além disso, note que aparecem duas medidas a respeito da qualidade da predição realizada. Para entendê-las, considere a tabela abaixo:
\begin{center}
\begin{tabular}{lccc}\cline{2-4}
& & \multicolumn{2}{c}{Verdade} \ \hline
& & Sim & Não \
\multirow{2}{*}{Predição} & Sim & \(a\) & \(b\) \
& Não & \(c\) & \(d\) \ \hline
\end{tabular}
\end{center}
Em um modelo de classificação, que desejamos é que os valores da diagonal da tabela sejam os maiores possíveis e os valores fora da diagonal sejam os menores possíveis. Estes valores são tão importantes que eles possuem nomes próprios:
-
\(a\): verdadeiro positivo -
\(b\): falso negativo -
\(c\): falso positivo -
\(d\): verdadeiro negativo
Assim, temos as seguintes medidas para avaliar o quão boa foi nossa predição:
$$\textrm{Accuracy} = p_0 = \frac{a+d}{a+b+c+d}$$
e
$$ Kappa: \begin{align*} p_{\mbox{Sim}} & = \frac{a+b}{a+b+c+b} \times \frac{a+c}{a+b+c+b} \ p_{\mbox{Não}} & = \frac{c+d}{a+b+c+b} \times \frac{b+d}{a+b+c+b} \ p_e & = p_{\mbox{Sim}} + p_{\mbox{Não}} \ \end{align*} $$
Com estas medidas definidas, o Kappa é dado por
$$Kappa = \frac{p_0-p_e}{1-p_e}.$$
Para não me alongar ainda mais, vou deixar a explicação da acurácia e do Kappa em aberto, mas basta saber que tanto a acurácia quanto o Kappa variam entre 0 e 1. Não obstante, quanto maiores estes valores, melhor é o ajuste do modelo.
Finalizamos o ajuste testando se este modelo criado é capaz de classificar novos dados. Para isto, vamos utilizar o conjunto de teste definido anteriormente:
predicao <- predict(ajuste_iris, iris_teste)
confusionMatrix(predicao, iris_teste$especie)
## Confusion Matrix and Statistics
##
## Reference
## Prediction setosa versicolor virginica
## setosa 12 0 0
## versicolor 0 12 4
## virginica 0 0 8
##
## Overall Statistics
##
## Accuracy : 0.8889
## 95% CI : (0.7394, 0.9689)
## No Information Rate : 0.3333
## P-Value [Acc > NIR] : 6.677e-12
##
## Kappa : 0.8333
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: setosa Class: versicolor Class: virginica
## Sensitivity 1.0000 1.0000 0.6667
## Specificity 1.0000 0.8333 1.0000
## Pos Pred Value 1.0000 0.7500 1.0000
## Neg Pred Value 1.0000 1.0000 0.8571
## Prevalence 0.3333 0.3333 0.3333
## Detection Rate 0.3333 0.3333 0.2222
## Detection Prevalence 0.3333 0.4444 0.2222
## Balanced Accuracy 1.0000 0.9167 0.8333
A função confusionMatrix apresenta diversas estatísticas a respeito das previsões que realizamos. Note que apenas uma flor da espécie Iris virginica foi classificada de maneira inadequada. Todas as outras foram classificadas corretamente. Além disso, a acurácia está bastante alta, igual a 0,9722. O Kappa igual a 0,9583 também não é de se desprezar.
Portanto, podemos concluir este projeto dizendo que fomos bem sucedidos ao utilizar o Random Forest para classificar as espécies de plantas de acordo com as variáveis comprimento e largura da sépala e comprimento e largura da pétala.
Para finalizar, podemos verificar quais foram, dentre estas quatro variáveis preditoras, aquelas que tiveram a maior importância no modelo.
ggplot(varImp(ajuste_iris))
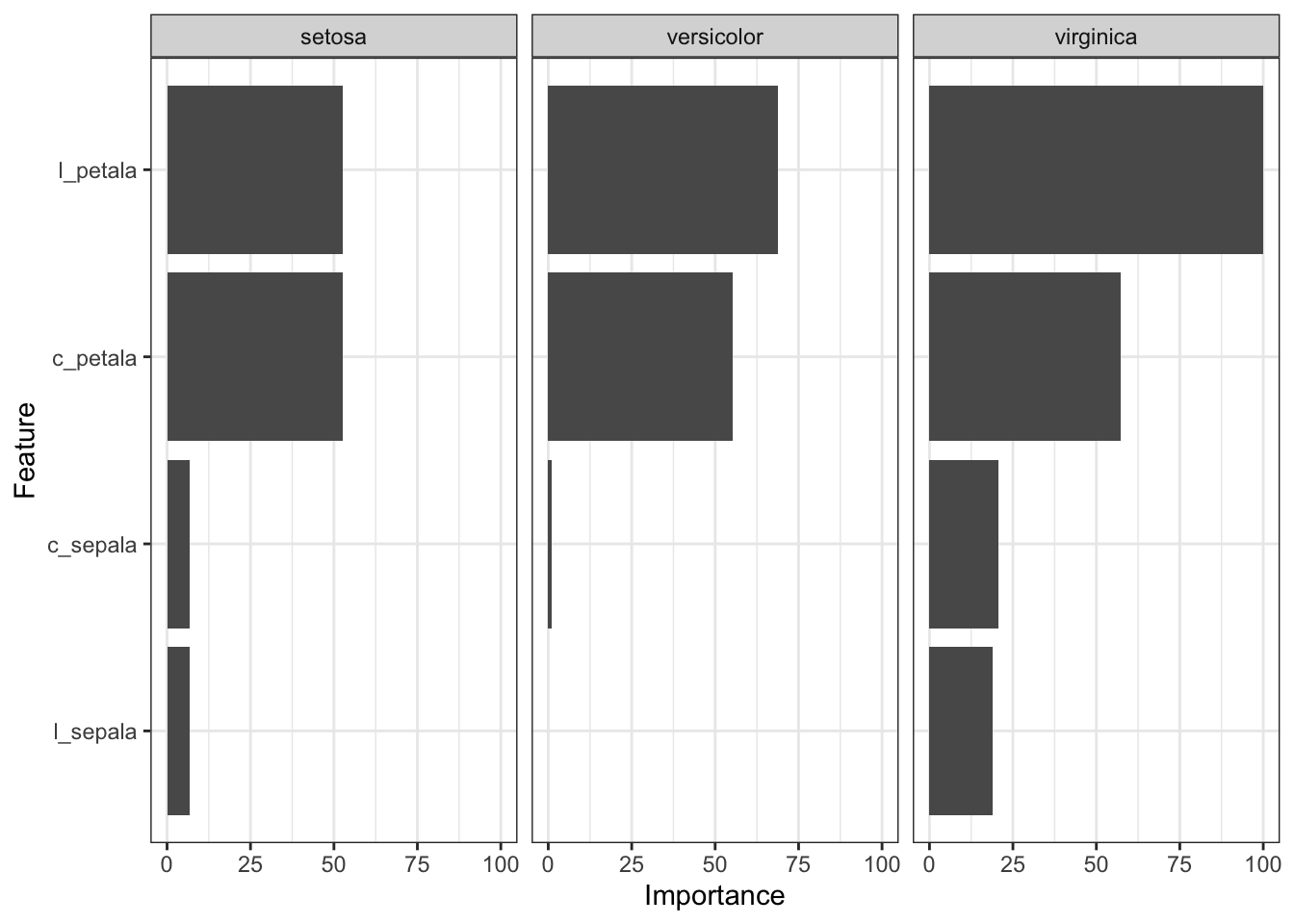
Como podemos ver, as variáveis relacionadas à pétala são mais importantes do que as variáveis relacionadas à sépala. Além disso, em termos de importância, a largura da pétala parece levar ligeira vantagem em relação ao comprimento.
Ideias para Novos Projetos Link para o cabeçalho
Este texto que publiquei não toca em vários assuntos concernentes ao ajuste de modelos de machine learning. Por exemplo, eu não comentei sobre paralelização de código, não fui a fundo na descrição do modelo e não falei sobre o tuning dos hiperparâmetros da Random Forest. Tratarei destes assuntos em outra oportunidade.
Obter dados para análise é algo trivial hoje em dia. Existem diversos sites que disponibilizam todo tipo de dados para as mais diversas tarefas. Abaixo eu listo algumas das minhas fontes preferidas para buscar dados abertos, colocadas mais ou menos em ordem de preferência e importância:
-
Kaggle: Acredito que este seja, atualmente, o maior site sobre machine learning no mundo. Possui muitos conjuntos de dados disponíveis, nas mais variadas áreas. Além dos dados, há diversos projetos de machine learning já realizados nele, fazendo com que seja uma fonte quase inesgotável de informação.
-
UCI Machine Learning Repository: Este é o pai do Kaggle. Na época em que fiz meu primeiro curso de data mining, ainda durante meu doutorado no longínquo ano de 2010, este site era minha fonte principal de conjuntos de dados para classificação e clusterização.
-
Instituto Brasileiro de Geografia e Estatística (IBGE): O site do IBGE disponibiliza informações sobre os censos, PNAD e tudo mais que o IBGE trabalha.
-
Portal Brasileiro de Dados Abertos: Informações oficiais do governo brasileiro sobre mapas, orçamento da união, aviação, dentre outros assuntos.
-
Portal da Transparência: Dados do executivos brasileiro, como salários, pagamentos de programas sociais e muito mais.
Além destas fontes de terceiros, eu mantenho uma lista de favoritos online, locais em que encontrei fontes interessantes para dados. Venho fazendo isto desde 2007. Os links são os seguintes:
Espero que estas informações sejam uteis para vocês. Esta lista não esgota todas as boas fontes de dados abertos na internet. Há muitas outras, tão boas quanto estas que listei, que podem ser encontradas em .
Caso alguma fonte de dados óbvia tenha faltado, comente aí embaixo que eu atualizo o post com ela.
Agora que o seu primeiro projeto de data science está completo, o céu é o limite. Leia livros sobre o assunto, me contrate para te dar um curso mais avançado ou simplesmente visite o Kaggle e escolha um novo assunto de seu interesse para trabalhar.