Creio que as duas imagens mais marcantes em toda a história do programa espacial norte-americano sejam a caminhada de Neil Armostrong na Lua e a explosão do ônibus espacial Challenger. Esta tragédia, exibida ao vivo pela TV em 28 de janeiro de 1986, chocou o mundo.
Após uma cuidadosa investigação, a NASA concluiu que a explosão ocorreu devido ao mau funcionamento de uma peça chamada O-ring, que deveria manter a junção entre as partes dos foguetes que levariam a Challenger para o espaço. Mas será que o problema com estas peças não poderia ter sido previsto utilizando dados dos outros lançamentos de ônibus espaciais?
A Challenger foi a 25a missão oficial de um ônibus espacial. Para fazer este estudo, utilizei os dados de temperatura e falhas de O-rings de 23 voos de ônibus espaciais anteriores ao da Challenger, obtidos no UCI Machine Learning Repository. Apenas os dados de 23 dos 24 voos anteriores estão disponíveis publicamente.
O gráfico abaixo mostra, no eixo horizontal, as temperaturas de lançamento, em graus Celsius, durante o lançamento dos ônibus espaciais. No eixo vertical, 0 significa que não houve problemas com nenhum O-ring durante o lançamento do ônibus espacial naquela temperatura e 1 significa que houve algum problema com pelo menos um O-ring durante o lançamento.
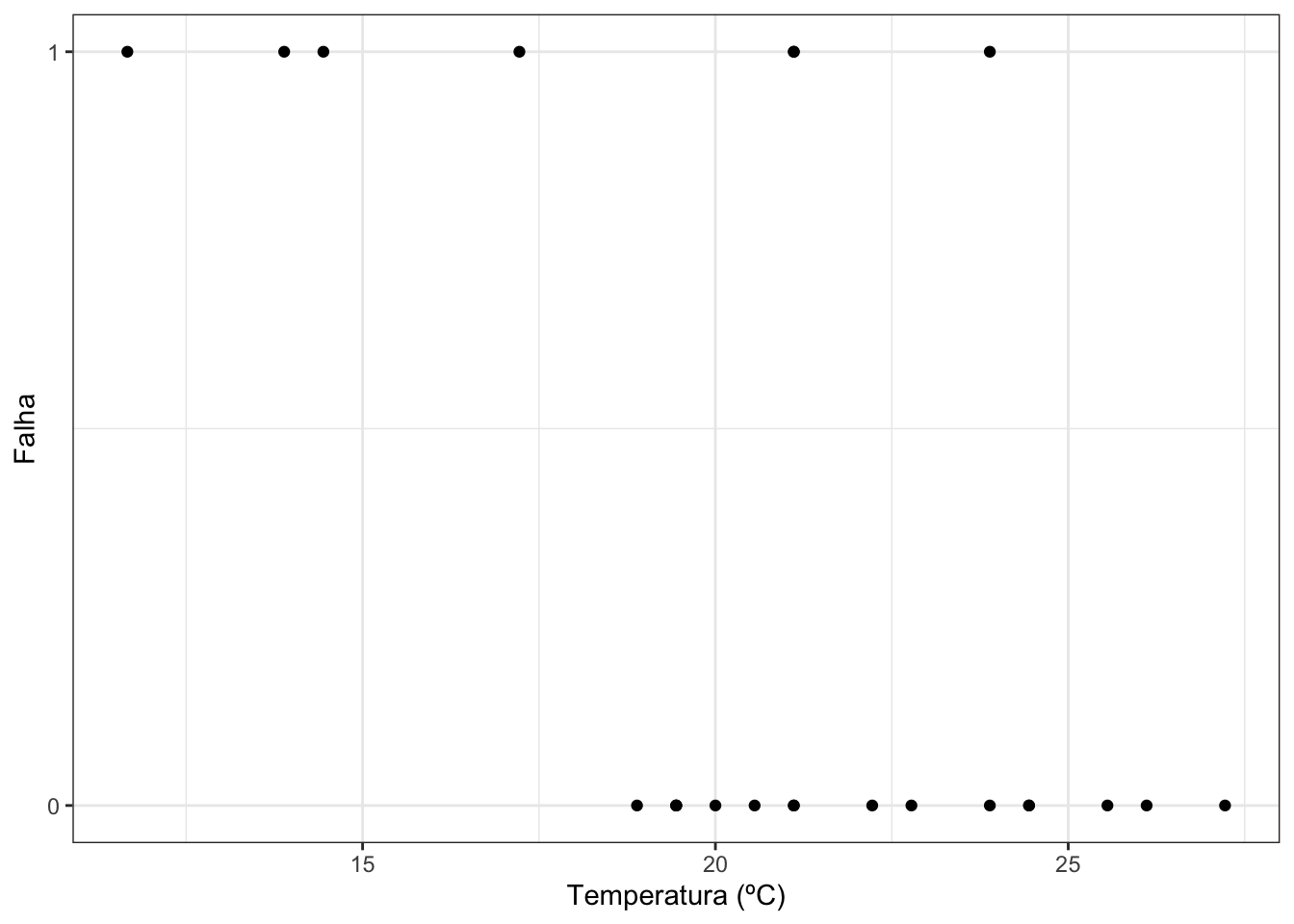
Perceba que, aparentemente, há influência da temperatura no comportamento dos O-rings. Quanto mais frio, é mais provável que haja algum problema com o dispositivo. Mas estatística não é achismo e há uma maneira de testar se esta hipótese é verdadeira. Para isto, utilizei uma ferramenta chamada regressão logística. O R, software que utilizo no meu dia a dia, possui um comando específico para isto, chamado glm. A resposta que obtive está logo abaixo:
ajuste <- glm(falha ~ temperatura, data=dados, family=binomial)
summary(ajuste)
##
## Call:
## glm(formula = falha ~ temperatura, family = binomial, data = dados)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 7.6137 3.9334 1.936 0.0529 .
## temperatura -0.4179 0.1948 -2.145 0.0320 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 28.267 on 22 degrees of freedom
## Residual deviance: 20.315 on 21 degrees of freedom
## AIC: 24.315
##
## Number of Fisher Scoring iterations: 5
Mas o que este monte de números quer realmente dizer? Vejamos como a curva dada pelo output acima se ajusta à realidade:
## `geom_smooth()` using formula = 'y ~ x'
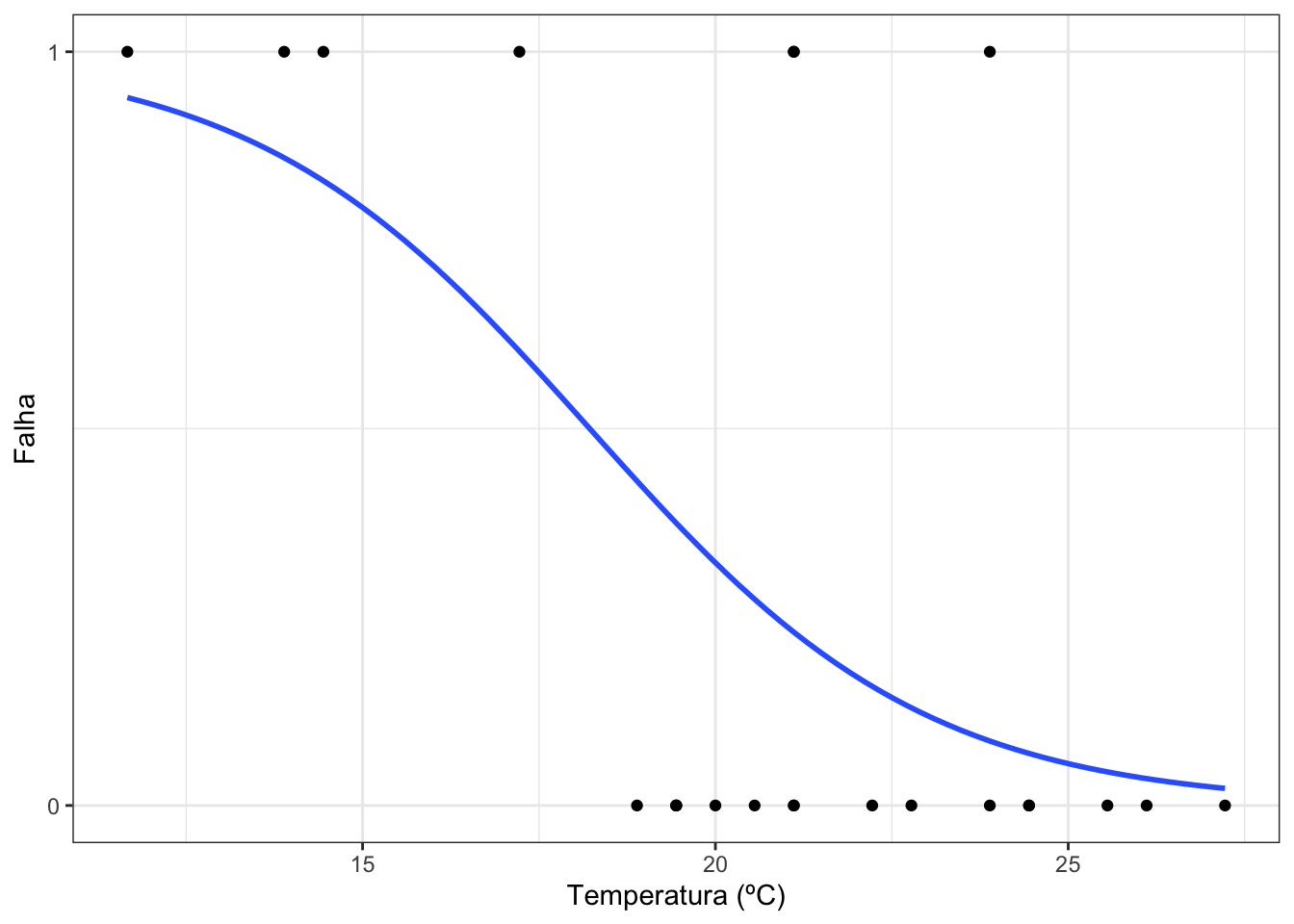
Nesta figura, além do eixo y indicar se houve ou não algum problema com os o-rings, ele indica a probabilidade de haver um acidente dada a temperatura do local do lançamento do ônibus espacial. No dia do lançamento da Challenger, a temperatura estava prevista para 31°F (equivalente a -0,5ºC). Até então, esta seria a temperatura mais baixa de lançamento de um ônibus espacial. Substituindo um valor próximo a este e outros no modelo ajustado acima, temos as seguintes probabilidades de falha do o-ring:
## temperatura probabilidade
## 1 0 0.9995065985
## 2 5 0.9960269060
## 3 10 0.9687735209
## 4 15 0.7933601306
## 5 20 0.3220940541
## 6 25 0.0555337160
## 7 30 0.0072240135
## 8 35 0.0008996910
## 9 40 0.0001114276
Note que, para temperaturas próximas de zero, a probabilidade de falha é muito próxima de 1. Ou seja, a chance de falha é de quase 100%! Se a temperatura estivesse mais alta, acima de 25 graus, esta probabilidade cairia para 0,055 (puco mais de 5%). Ou seja, a falha do equipamento era quase uma certeza.
Por si só, a falha de um ou mais O-rings não acarretaria na explosão da nave. Entretanto, não era necessário arriscar a vida de sete astronautas e um equipamento caríssimo num lançamento muito propenso a ter problemas. Bastaria esperar alguns dias por condições mais propícias para este realizar este evento.
Os arquivos e códigos utilizados nesta análise podem ser encontrados no meu github.