Um dos tipos de trabalho que aparece mais frequentemente no Laboratório de Consultoria que coordeno na universidade diz respeito à análise de questionários. Recebemos pedidos de colaboração na preparação dos questionários, cálculo do tamanho amostral para sua aplicação e análise dos resultados coletados.

Em geral, nossos clientes estão interessados apenas em estatísticas descritivas básicas a respeito dos resultados obtidos em suas pesquisas. Sendo assim, o intuito deste meu post é mostrar que há um outro mundo possível para quem deseja obter informações mais sofisticadas a respeito dos questionários que aplica em seus sujeitos. Para ilustrar estas ideias, compartilho o código de uma análise de questionário realizada por mim no software R.

Questionário Link para o cabeçalho

Um questionário aplicado a 13156 sujeitos se propôs a avaliar o que estas pessoas achavam de uma série de preceitos morais. Foram feitas 20 afirmações que deveriam ser respondidas de acordo com uma escala Likert, definida da seguinte maneira:

Discordo totalmente
Discordo parcialmente
Indiferente
Concordo parcialmente
Concordo totalmente

Caso o respondente não soubesse classificar alguma informação, ele poderia responder 0. As afirmações feitas foram as seguintes:

Q01. Nunca conte as suas reais intenções a respeito de algo que você fez a não ser que seja útil fazer isso.
Q02. A melhor maneira de lidar com pessoas é falando o que elas desejam ouvir.
Q03. As pessoas devem agir apenas quando é moralmente correto.
Q04. A maioria das pessoas é boa e gentil.
Q05. É mais seguro assumir que todas as pessoas possuem um lado mau e ele virá à nota quando houver oportunidade.
Q06. Honestidade é um princípio a ser adotado em todas as situações.
Q07. Não há desculpa para mentir.
Q08. De maneira geral, as pessoas não vão trabalhar duro a não ser que sejam forçadas a isso.
Q09. De modo geral, é melhor ser modesto e honesto do que arrogante e desonesto.
Q10. Quando você pede para alguém fazer algo para você é melhor dar a verdadeira razão do pedido do que dar razões que sejam particularmente mais fortes para quem as ouve.
Q11. A maioria das pessoas que chegam longe na vida são honestas, possuindo vidas limpas e de acordo com a moral.
Q12. Qualquer pessoas que acredite seriamente nos outros está pedindo para ter problemas.
Q13. A principal diferença entre a maioria dos criminosos e as outras pessoas é que os criminosos são estúpidos o suficiente para terem sido pegos.
Q14. A maioria das pessoas é corajosa.
Q15. É sábio elogiar pessoas importantes.
Q16. É possível ser bom em todos os aspectos.
Q17. A autor da frase “nasce um otário a cada minuto” estava errado.
Q18. É difícil chegar longe na vida sem tomar alguns atalhos aqui e ali.
Q19. Pessoas que sofrem de doenças incuráveis deveria ter a escolha de optar por serem mortas sem dor.
Q20. A maioria das pessoas esquecerá mais fácil a morte dos seus pais do que a perda do seu patrimônio.

Além destas, outras variáveis foram coletadas:

score: variando de 20 a 100, é um índice calculado a partir das respostas dos sujeitos às aformações Q01 a Q20
genero: 1 para masculino, 2 para feminino, 3 para outro, 0 sem resposta
idade: idade de cada sujeito, em anos
tempo_decorrido: tempo, em segundos, que cada sujeito levou para responder ao questionário

Os dados brutos podem ser obtidos através deste link.

Preparação dos Dados Link para o cabeçalho

Antes de proceder com a análise em si, é necessário preparar os dados. Todo mundo que já aplicou um questionário, principalmente via internet, sabe que o maior problema depois da não-resposta é a falta de compromisso de alguns respondentes. É muito difícil localizar respostas dadas de maneira deliberadamente equivocada para as questões de um questionário. Em geral, confiamos na boa-fé de quem responde.

Entretanto, outras perguntas pode ser utilizadas como balizas do que podemos ou não confiar naquilo que estamos analisando. Pensando nisso e de modo a ter um questionário o mais fiel possível à realidade, vamos remover do conjunto de dados analisado todo sujeito que satisfaça pelo menos uma das condições abaixo:

i. respondeu 0 para ao menos uma afirmação

ii. idade inferior a 18 anos

iii. idade superior a 90 anos

iv. tempo de resposta do questionário superior à média mais três desvios padrão dos demais respondentes

O código para fazer isto neste conjunto de dados é o seguinte:

library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.0     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

theme_set(theme_bw())
library(reshape2)

## 
## Attaching package: 'reshape2'
## 
## The following object is masked from 'package:tidyr':
## 
##     smiths

# leitura dos dados

maquiavel <- read.csv(file = "maquiavel.csv")

# limpeza dos dados de acordo com as regras acima

maquiavel <- maquiavel %>%
  # i
  mutate(across(starts_with("Q"), ~na_if(., 0))) %>%
  na.omit() %>%
  # ii
  filter(idade >= 18) %>%
  # iii
  filter(idade <= 90) %>%
  # iv
  filter(tempo_decorrido <= (mean(tempo_decorrido) + (3*sd(tempo_decorrido))))

dim(maquiavel)

## [1] 10881    24

No final, ficamos com 20 respostas de 10875 sujeitos. E agora, com o conjunto de dados limpo, é possível proceder com a análise exploratória.

Análise Exploratória Link para o cabeçalho

A primeira análise que faço é a da comparação da proporção de respostas para cada pergunta. Abaixo eu mostro como fazer isso de maneira prática no R, além de exibir o resultado que obtive para este problema.

maquiavel %>%
  select(-idade, -genero, -score, -tempo_decorrido) %>% 
  melt() %>% 
  group_by(variable, value) %>%
  count() %>%
  group_by(variable) %>%
  mutate(prop = n/sum(n)) %>%
  ggplot(., aes(x = variable, y = prop, fill = factor(value, levels = 5:1))) +
  geom_col() +
  coord_flip() +
  labs(x = "Pergunta", y = "Proporção", fill = "Resposta") +
  scale_fill_viridis_d()

## No id variables; using all as measure variables

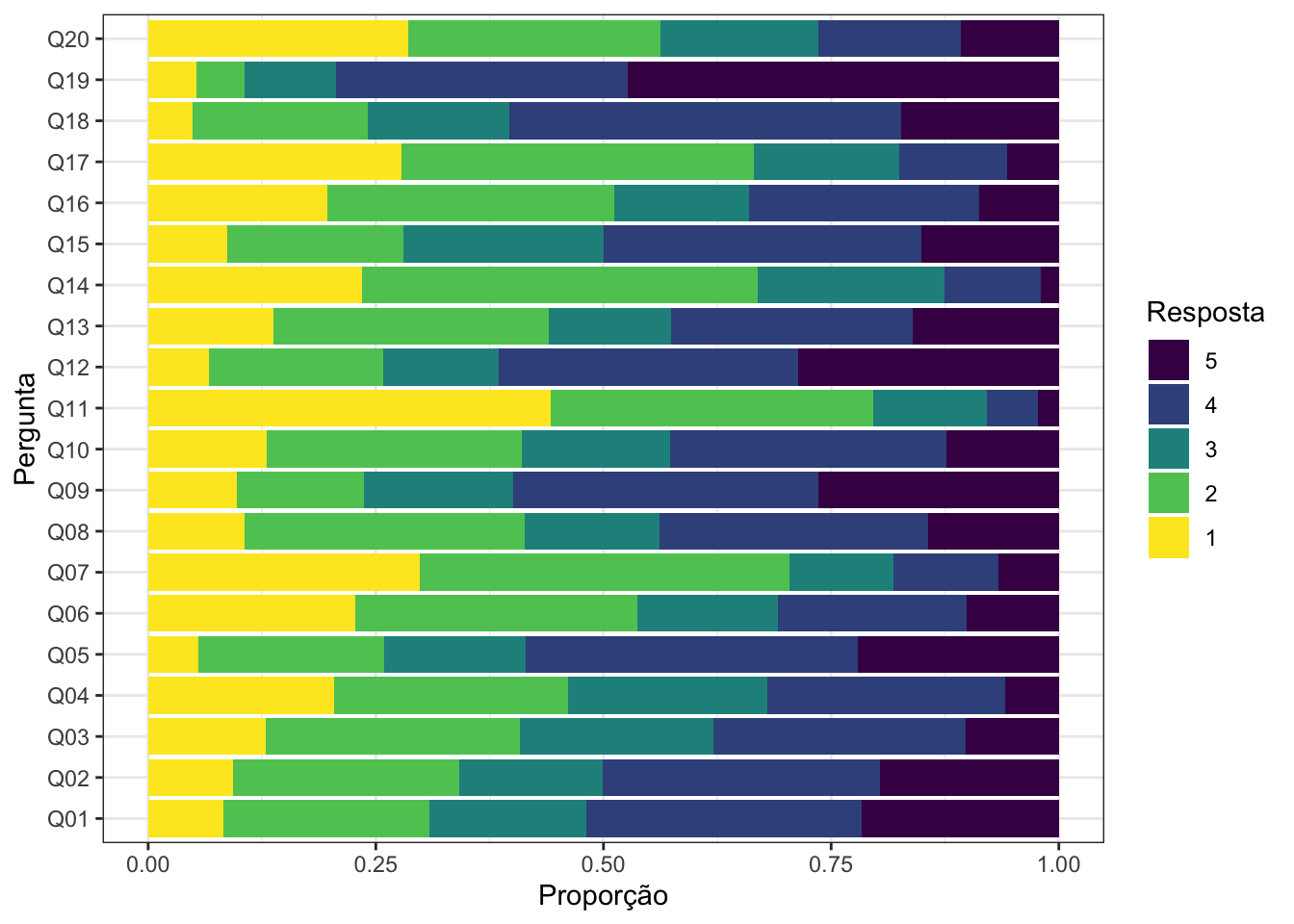
A primeira coisa que podemos perceber neste conjunto de dados é que se em dada pergunta a proporção de respostas 1 é grande, a proporção de respostas 5 é pequena e vice-versa. Para o primeiro caso, veja o comportamento das questões Q07, Q11 e Q20. Para o segundo caso, as questões Q01, Q02 e Q05 são bons exemplos.

Com a análise exploratória realizada, é hora de procedermos com a análise fatorial deste questionário.

Análise Fatorial Link para o cabeçalho

Isto nos leva a perguntar se seria possível agrupar as questões realizadas. Ou seja, será que é possível utilizar menos do que 20 questões para descrever o perfil psicológico das pessoas que responderam este questionário? Em outras palavras, como podemos simplificar este resultado e obter uma maneira direta de classificar os seus respondentes?

Uma forma de fazer isto é através da análise de componentes principais. Ao fazermos ela, obtemos uma sugestão de quantas variáveis latentes devemos utilizar em nossa análise fatorial. Entretanto, só podemos usar os resultados das questões para fazer a análise fatorial: todas as outras variáveis devem ser retiradas do conjunto de dados.

maquiavel_questoes <- maquiavel %>%
  select(-idade, -genero, -score, -tempo_decorrido)

pca <- prcomp(maquiavel_questoes, center = TRUE, scale. = TRUE)

summary(pca)

## Importance of components:
##                           PC1     PC2     PC3     PC4     PC5     PC6     PC7
## Standard deviation     2.5696 1.27574 1.09396 0.98361 0.94059 0.89596 0.86147
## Proportion of Variance 0.3301 0.08138 0.05984 0.04837 0.04424 0.04014 0.03711
## Cumulative Proportion  0.3301 0.41151 0.47135 0.51972 0.56396 0.60410 0.64120
##                            PC8     PC9    PC10    PC11    PC12    PC13    PC14
## Standard deviation     0.83451 0.81821 0.80674 0.78658 0.76874 0.76320 0.75608
## Proportion of Variance 0.03482 0.03347 0.03254 0.03094 0.02955 0.02912 0.02858
## Cumulative Proportion  0.67602 0.70950 0.74204 0.77297 0.80252 0.83165 0.86023
##                          PC15    PC16    PC17    PC18    PC19   PC20
## Standard deviation     0.7403 0.72338 0.70958 0.67544 0.63913 0.5966
## Proportion of Variance 0.0274 0.02616 0.02518 0.02281 0.02042 0.0178
## Cumulative Proportion  0.8876 0.91379 0.93897 0.96178 0.98220 1.0000

plot.pca <- data.frame(
  x = 1:20,
  y = unlist(as.data.frame(summary(pca)[6])[1, ])
)

plot.pca %>%
  head(10) %>%
  ggplot(., aes(x = x, y = y^2)) +
  geom_line() +
  labs(x = "Componente Principal", y = "Variância") +
  scale_colour_viridis_d() +
  scale_x_continuous(breaks = 1:10, minor_breaks = 1:10)

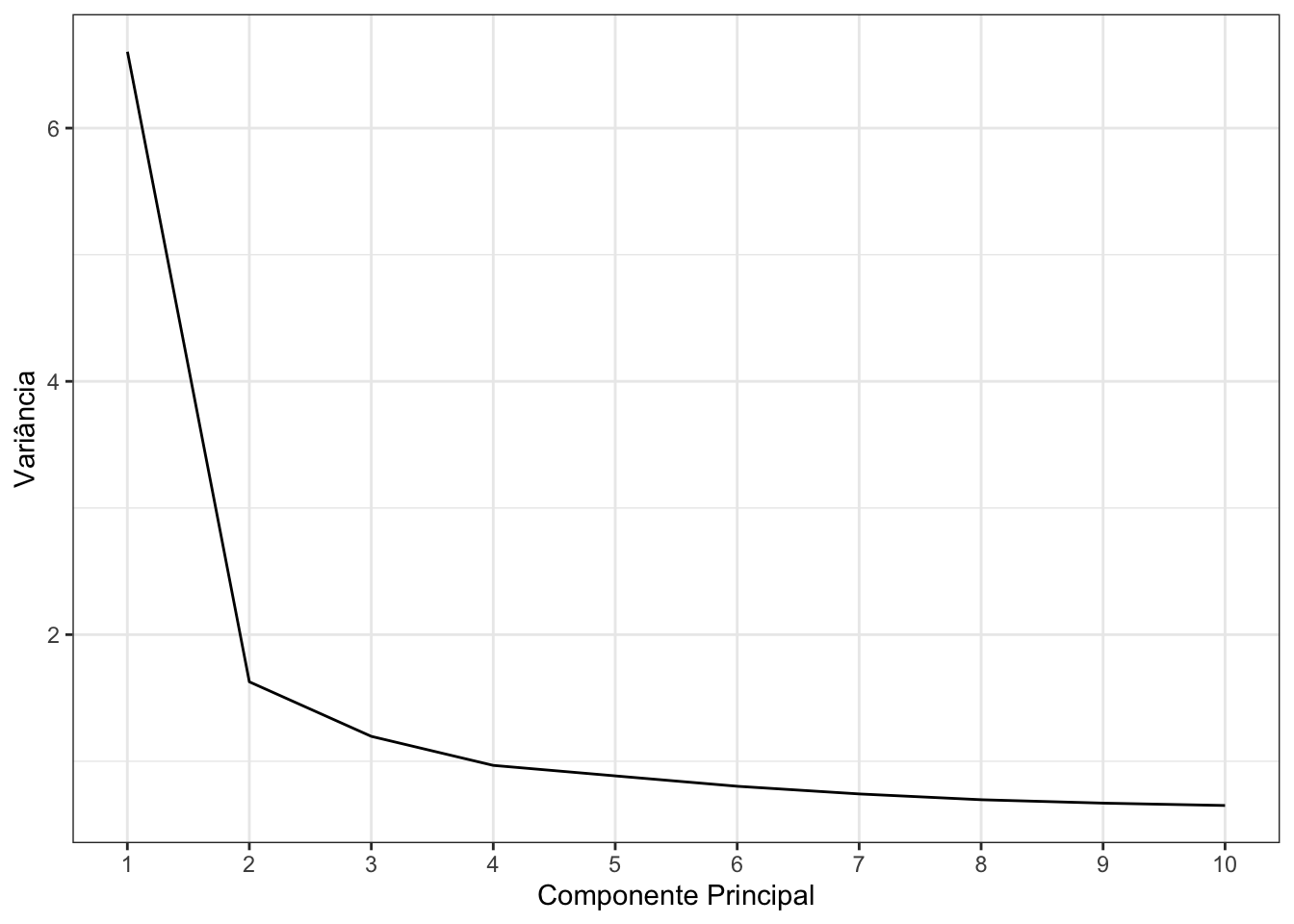
Pelo gráfico acima, vemos que a variância estabiliza por volta da terceira ou quarta componente principal. Sendo assim, vou criar a representação gráfica da análise fatorial com quatro variáveis latentes:

ajuste_4 <- factanal(maquiavel_questoes, 
                     factors = 4,
                     scores = c("regression"),
                     rotation = "none")

ajuste_4

## 
## Call:
## factanal(x = maquiavel_questoes, factors = 4, scores = c("regression"),     rotation = "none")
## 
## Uniquenesses:
##   Q01   Q02   Q03   Q04   Q05   Q06   Q07   Q08   Q09   Q10   Q11   Q12   Q13 
## 0.539 0.527 0.609 0.541 0.586 0.377 0.369 0.619 0.327 0.514 0.622 0.599 0.558 
##   Q14   Q15   Q16   Q17   Q18   Q19   Q20 
## 0.609 0.674 0.735 0.832 0.692 0.877 0.722 
## 
## Loadings:
##     Factor1 Factor2 Factor3 Factor4
## Q01 -0.618   0.257                 
## Q02 -0.592   0.180   0.229   0.194 
## Q03  0.553   0.202           0.212 
## Q04  0.566           0.322   0.170 
## Q05 -0.538   0.325  -0.126         
## Q06  0.697   0.360                 
## Q07  0.623   0.446          -0.210 
## Q08 -0.485   0.381                 
## Q09  0.729          -0.226   0.290 
## Q10  0.672   0.107  -0.133         
## Q11  0.499   0.113   0.339         
## Q12 -0.552   0.268  -0.136         
## Q13 -0.573   0.336                 
## Q14  0.528           0.331         
## Q15 -0.478   0.114   0.248   0.152 
## Q16  0.465   0.132   0.168         
## Q17  0.343           0.201         
## Q18 -0.518   0.171           0.101 
## Q19 -0.308                   0.149 
## Q20 -0.430   0.290                 
## 
##                Factor1 Factor2 Factor3 Factor4
## SS loadings      6.011   1.091   0.630   0.340
## Proportion Var   0.301   0.055   0.031   0.017
## Cumulative Var   0.301   0.355   0.387   0.404
## 
## Test of the hypothesis that 4 factors are sufficient.
## The chi square statistic is 1417.64 on 116 degrees of freedom.
## The p-value is 1.18e-222

grafico <- as.data.frame(ajuste_4$loadings[, 1:2])

ggplot(grafico, aes(x = Factor1, y = Factor2)) +
  geom_text(label=rownames(grafico)) +
  labs(x = "Fator 1", y = "Fator 2") +
  scale_colour_viridis_d()

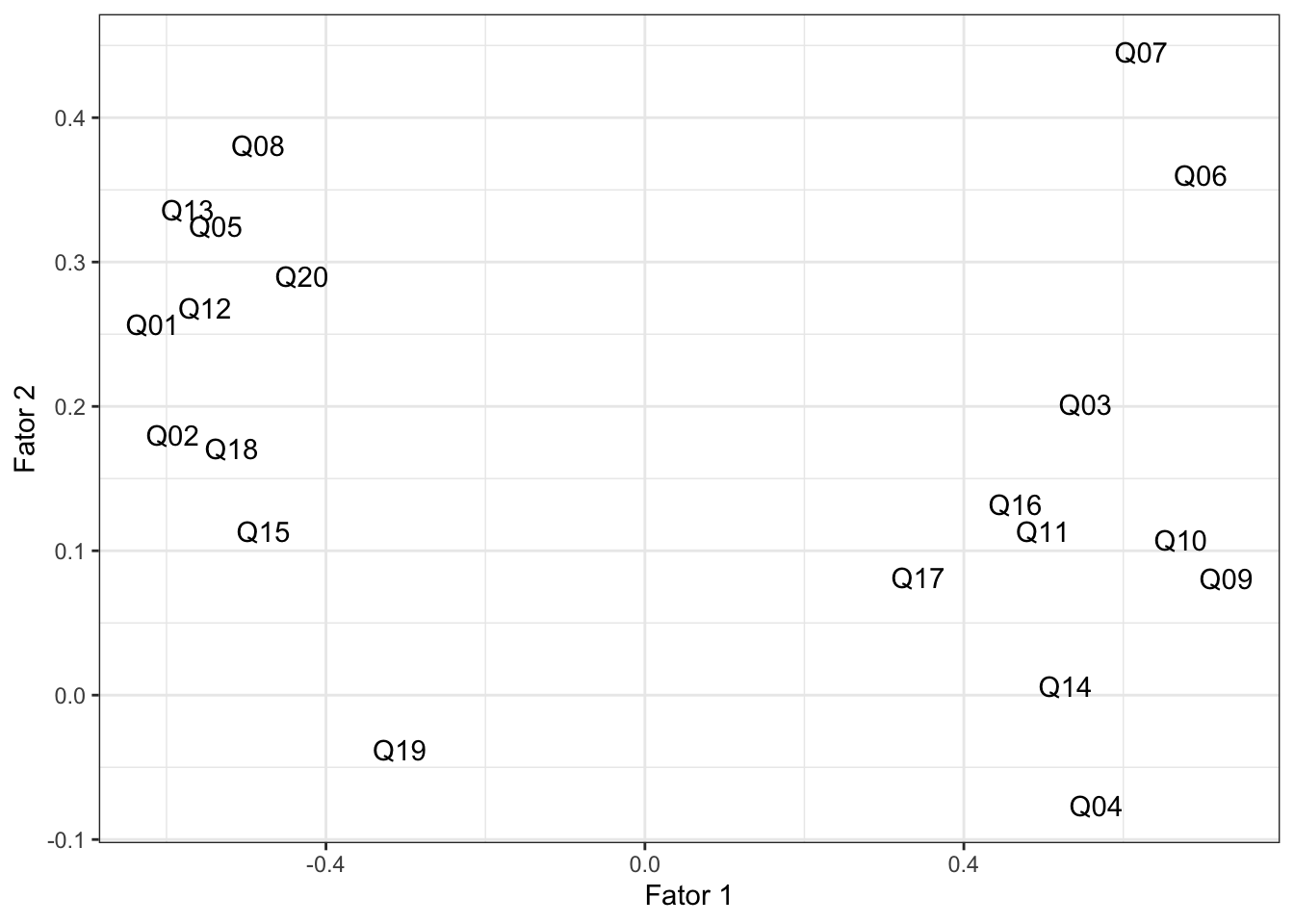
Note como há quatro grupos bem definidos no gráfico. Separando-os por proximidade e me baseando nas questões definidas no começo deste post, eu os nomeria da seguinte maneira:

manipulação: Q01, Q02, Q05, Q08, Q12, Q13, Q15, Q18, Q20
bondade: Q03, Q04, Q09, Q10, Q11, Q14, Q16, Q17
honestidade: Q06, Q07
compaixao: Q19

Ou seja, podemos reduzir oito questões (Q01, Q02, Q05, Q08, Q12, Q13, Q15, Q18, Q20) a apenas uma qualidade: manipulação. Parece-me que estas questões tratam todas, em maior ou menor grau, do mesmo assunto. Resultados similares podem ser deduzidos para as demais variáveis e questões aplicadas.

Conclusão Link para o cabeçalho

Conseguimos pegar um questionário com 20 questões, que é algo bastante complexo, e reduzi-lo para quatro variáveis latentes. Uma ferramenta assim é muito útil para resumir informações obtidas a partir de questionários aplicados aos mais diversos sujeitos.