Introdução Link para o cabeçalho

O paradoxo de Simpson aparece quando temos um conjunto de dados com uma tendência bem definida quando considerado completo, mas que muda completamente quando é separado em grupos.

Visualização do Paradoxo de Simpson Link para o cabeçalho

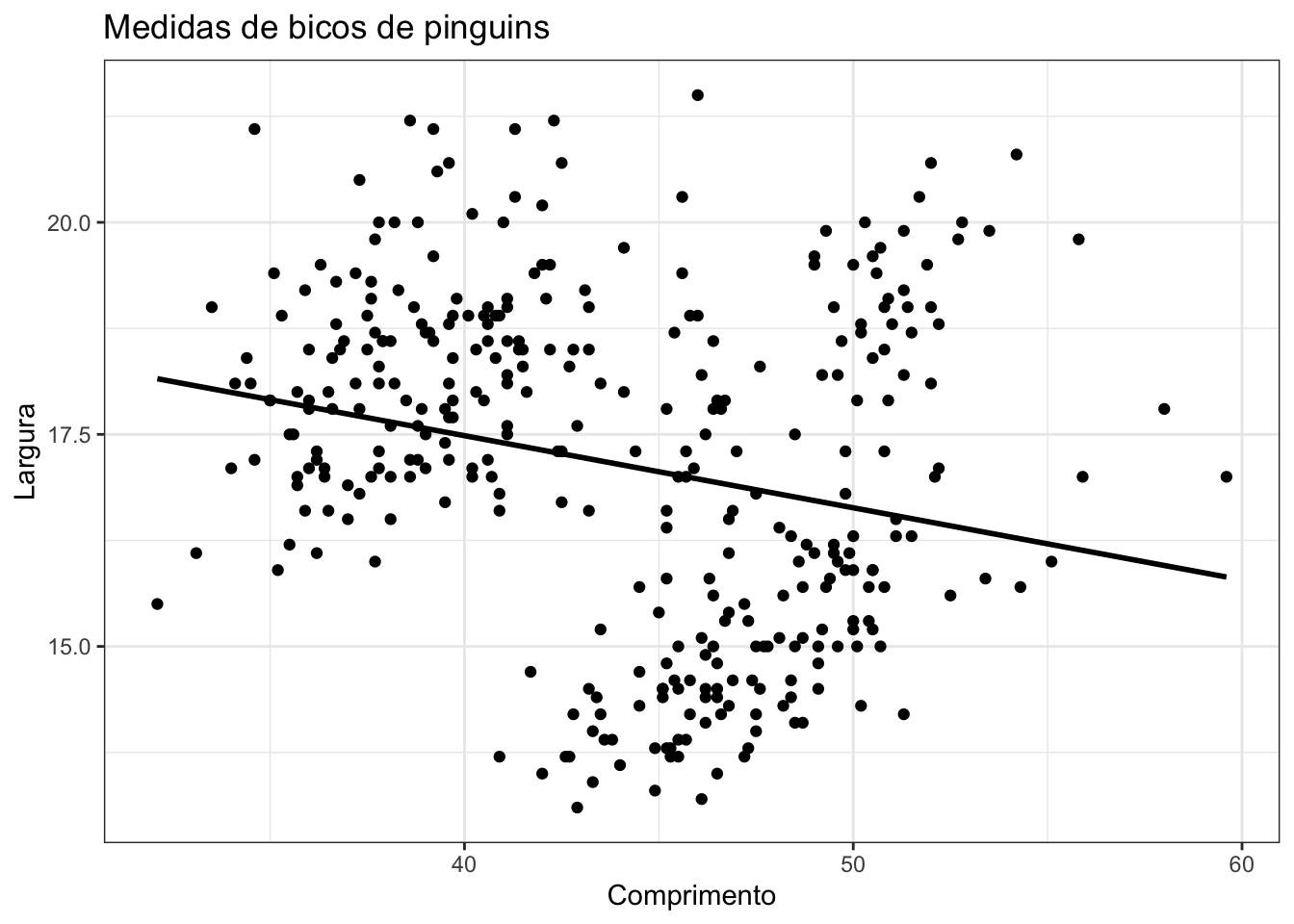
A melhor maneira de entender o que é o paradoxo de Simpson é visualizando-o na prática. A Figura a seguir mostra um gráfico de dispersão entre comprimento e largura de bicos de pinguins.

library(tidyverse)

## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr     1.1.4     ✔ readr     2.1.5
## ✔ forcats   1.0.0     ✔ stringr   1.5.1
## ✔ ggplot2   3.5.0     ✔ tibble    3.2.1
## ✔ lubridate 1.9.3     ✔ tidyr     1.3.1
## ✔ purrr     1.0.2     
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

theme_set(theme_bw())
library(broom)
library(palmerpenguins)

ggplot(penguins, aes(x = bill_length_mm, y = bill_depth_mm)) +
  geom_point() + 
  geom_smooth(method = "lm", se = FALSE, colour = "black") +
  labs(x = "Comprimento", y = "Largura", title = "Medidas de bicos de pinguins")

## `geom_smooth()` using formula = 'y ~ x'

penguins %>%
  do(tidy(lm(bill_depth_mm ~ bill_length_mm, .)))

## # A tibble: 2 × 5
##   term           estimate std.error statistic  p.value
##   <chr>             <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)     20.9       0.844      24.7  4.72e-78
## 2 bill_length_mm  -0.0850    0.0191     -4.46 1.12e- 5

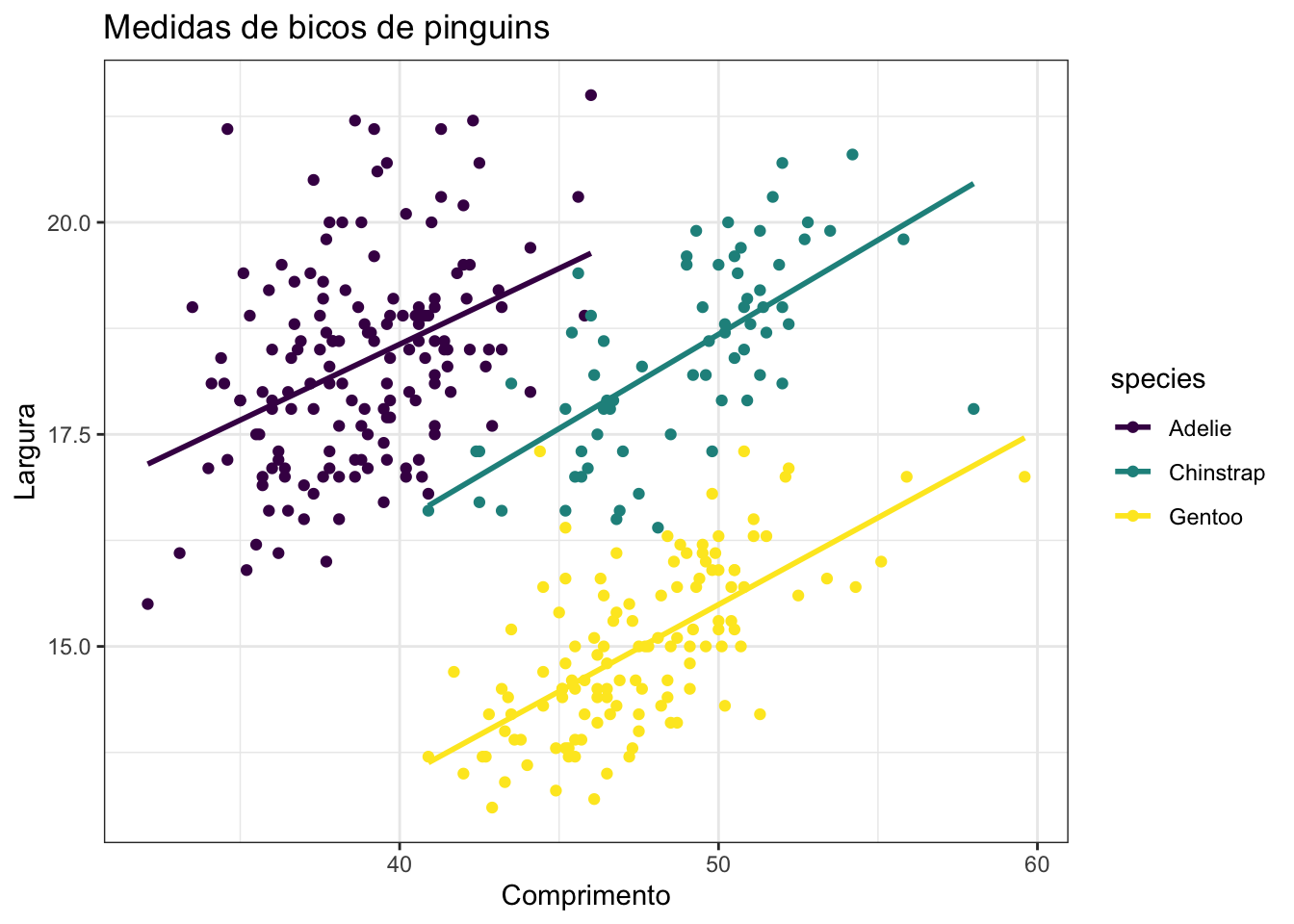
Como é possível ver acima, tanto gráfica quanto analiticamente, o coeficiente da regressão ajustada é negativo. Portanto, quanto mais comprido for o bico, menos largo ele será. Mas se criarmos uma regressão diferente para cada espécie de pinguim, o resultado obtido é diferente:

ggplot(penguins, 
       aes(x=bill_length_mm, 
           y=bill_depth_mm, 
           group = species, 
           colour = species)) +
  geom_point() + 
  geom_smooth(aes(colour = species), method = "lm", se = FALSE) +
  labs(x = "Comprimento", y = "Largura", title = "Medidas de bicos de pinguins", species = "Espécies") +
  scale_colour_viridis_d()

## `geom_smooth()` using formula = 'y ~ x'

penguins %>%
  group_by(species) %>%
  do(tidy(lm(bill_depth_mm ~ bill_length_mm, .)))

## # A tibble: 6 × 6
## # Groups:   species [3]
##   species   term           estimate std.error statistic  p.value
##   <fct>     <chr>             <dbl>     <dbl>     <dbl>    <dbl>
## 1 Adelie    (Intercept)      11.4      1.34        8.52 1.61e-14
## 2 Adelie    bill_length_mm    0.179    0.0344      5.19 6.67e- 7
## 3 Chinstrap (Intercept)       7.57     1.55        4.88 6.99e- 6
## 4 Chinstrap bill_length_mm    0.222    0.0317      7.01 1.53e- 9
## 5 Gentoo    (Intercept)       5.25     1.05        4.98 2.15e- 6
## 6 Gentoo    bill_length_mm    0.205    0.0222      9.24 1.02e-15

Perceba como as inclinações das retas se tornaram positivas, fato corroborado pelas equações das retas ajustadas a cada grupo.

Os códigos usados neste post podem ser baixados no meu github.