Introdução Link para o cabeçalho
Neste tutorial iremos comparar o desempenho da regressão linear e das random forests na predição de preços de automóveis usados fabricados pela Volkswagen e disponíveis no Reino Unido. Para isso, utilizaremos o conjunto de dados 100,000 UK Used Car Data set. Todos os arquivos utilizados nesta análise podem ser baixados no github, inclusive os conjuntos de dados.
EDA Link para o cabeçalho
# pacotes necessarios
library(tidyverse)
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ ggplot2 3.5.0 ✔ tibble 3.2.1
## ✔ lubridate 1.9.3 ✔ tidyr 1.3.1
## ✔ purrr 1.0.2
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ purrr::accumulate() masks foreach::accumulate()
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ✖ purrr::when() masks foreach::when()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
theme_set(theme_bw())
library(GGally)
## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2
# leitura dos dados
vw <- read_csv(file = "dados/vw.csv")
## Rows: 15157 Columns: 9
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr (3): model, transmission, fuelType
## dbl (6): year, price, mileage, tax, mpg, engineSize
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
Como em toda análise de dados, a primeira tarefa a ser realizada é a sua análise exploratória. Neste caso, quero verificar como está a relação entre as variáveis neste conjunto de dados, excetuando o modelo. Vou deixar esta variável de fora por enquanto, pois ela possui muitos níveis diferentes. Além disso, reordenei as colunas de modo que price fosse a primeira e, assim, a interpretação dos resultados ficasse mais simples. Note que, além disso, calculei a correlação de Spearman entre as variáveis, pois graficamente elas não apresentam linearidade ou normalidade.
vw %>%
select(-model) %>%
relocate(price) %>%
relocate(where(is.character), .after = last_col()) %>%
ggpairs(upper = list(continuous = wrap("cor", method = "spearman")))
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
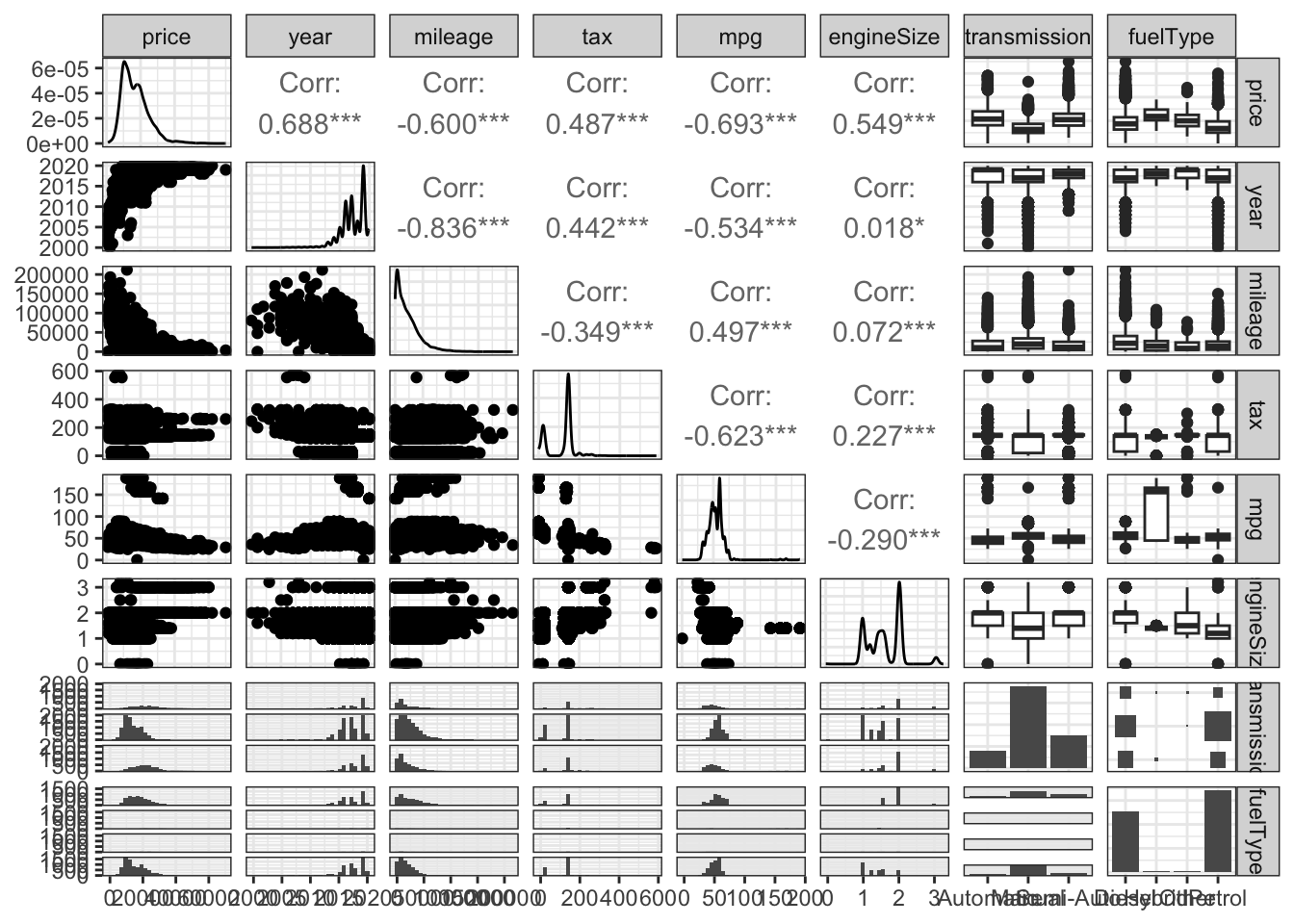
Este gráfico nos dá uma ideia de como o preço está correlacionado com as outras variáveis preditoras. A maior correlação positiva do preço ocorre em relação ao ano de fabricação do veículo. Quanto mais recente o carro, maior o seu preço. O mesmo vale para o imposto (tax) e tamanho do motor (engineSize). Intuitivamente, nenhuma destas relações me parece estar longe do esperado.
O preço está correlacionado negativamente em relação à milhagem (mileage) e consumo de combustível (mpg, sigla para miles per galon). Novamente, de forma intuitiva, estes resultados prévios parecem estar condizentes com o esperado para dados assim.
A relação do preço com as variáveis qualitativas não está muito clara. A diferença de nível parece pequena e com muitos outliers. Entretanto, devido ao grande volume de dados (15157 observações), é possível que as diferenças de nível vistas nos boxplots sejam significativas.
Preparação dos Dados Link para o cabeçalho
Antes de partir para a modelagem em si, é necessário que os dados sejam preparados. Neste caso, a minha modelagem inicial vai contar com três etapas:
- Limpeza dos Dados
- Divisão dos Dados em Treinamento e Teste
- Pré-Processamento das Variáveis Preditoras
Limpeza dos Dados Link para o cabeçalho
Como é possível ver nos gráficos criados pela nossa análise exploratória, há uma quantidade maior de carros fabricados nos últimos 5 anos do que nos anos menos recentes. Abaixo veremos o quão grande é esta disparidade:
vw %>%
group_by(year) %>%
count() %>%
ungroup() %>%
arrange(desc(year)) %>%
mutate(percentual = n/sum(n)*100,
acumulado = cumsum(percentual)) %>%
print(n = Inf)
## # A tibble: 21 × 4
## year n percentual acumulado
## <dbl> <int> <dbl> <dbl>
## 1 2020 1046 6.90 6.90
## 2 2019 4669 30.8 37.7
## 3 2018 1509 9.96 47.7
## 4 2017 2947 19.4 67.1
## 5 2016 2647 17.5 84.6
## 6 2015 1153 7.61 92.2
## 7 2014 580 3.83 96.0
## 8 2013 315 2.08 98.1
## 9 2012 80 0.528 98.6
## 10 2011 57 0.376 99.0
## 11 2010 41 0.271 99.3
## 12 2009 31 0.205 99.5
## 13 2008 27 0.178 99.6
## 14 2007 20 0.132 99.8
## 15 2006 16 0.106 99.9
## 16 2005 8 0.0528 99.9
## 17 2004 3 0.0198 99.9
## 18 2003 2 0.0132 100.
## 19 2002 1 0.00660 100.
## 20 2001 4 0.0264 100.
## 21 2000 1 0.00660 100
Como é possível ver, 92,2% dos carros foram fabricados de 2015 em diante. Ou seja, manter carros mais antigos do que esta data no conjunto de dados vai causar um desbalanceamento muito grande, prejudicandos os resultados. Além disso, se criarmos uma tabela que conte o número de modelos de carro por ano, a situação fica bem complicada:
vw %>%
select(year, model) %>%
group_by(year, model) %>%
count() %>%
ungroup() %>%
complete(year, model, fill = list(n = 0)) %>%
pivot_wider(names_from = "year", values_from = "n")
## # A tibble: 27 × 22
## model `2000` `2001` `2002` `2003` `2004` `2005` `2006` `2007` `2008` `2009`
## <chr> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
## 1 Amarok 0 0 0 0 0 0 0 0 0 0
## 2 Arteon 0 0 0 0 0 0 0 0 0 0
## 3 Beetle 0 3 0 1 0 1 3 3 0 1
## 4 Caddy 0 0 0 0 0 0 0 0 0 0
## 5 Caddy … 0 0 0 0 0 0 0 0 0 0
## 6 Caddy … 0 0 0 0 0 0 0 0 0 0
## 7 Caddy … 0 0 0 0 0 0 0 0 0 0
## 8 Califo… 0 0 0 0 0 0 0 0 0 0
## 9 Carave… 0 0 0 0 0 1 2 0 0 0
## 10 CC 0 0 0 0 0 0 0 0 0 0
## # ℹ 17 more rows
## # ℹ 11 more variables: `2010` <int>, `2011` <int>, `2012` <int>, `2013` <int>,
## # `2014` <int>, `2015` <int>, `2016` <int>, `2017` <int>, `2018` <int>,
## # `2019` <int>, `2020` <int>
Há uma quantidade de zeros muito grande na tabela construída. Graficamente, a situação é bastante clara:
vw %>%
select(year, model) %>%
group_by(year, model) %>%
count() %>%
ungroup() %>%
complete(year, model, fill = list(n = 0)) %>%
mutate(faltante = ifelse(n == 0, "Sim", "Não")) %>%
ggplot(., aes(x = year, y = model, fill = faltante)) +
geom_tile(colour = "white") +
labs(x = "Ano de Fabricação",
y = "Modelo do Carro",
fill = "Dado faltante?") +
scale_fill_viridis_d()
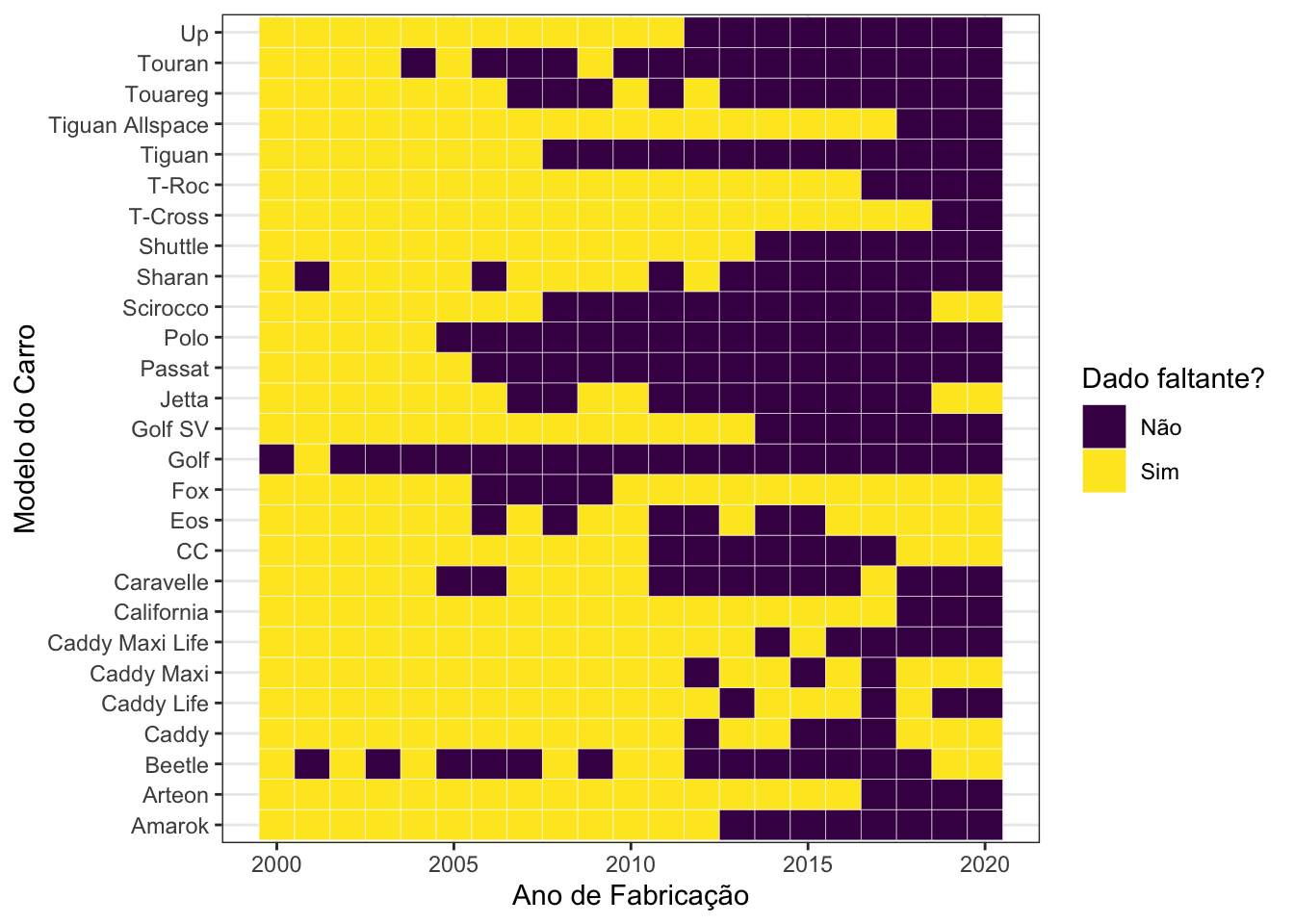
A grande quantidade de retângulos amarelos no gráfico acima mostra como há muitos dados faltantes. Em particular, 59,79% das combinações entre modelo de carro e ano não possuem nenhuma ocorrência. Por isso, baseado no fato de que 92,2% dos carros foram fabricados de 2015 em diante, vou restringir arbitrariamente este conjunto de dados para apenas os anos mais recentes, a partir desta data. Com isso, temos o seguinte:
vw_bk <- vw
vw <-
vw_bk %>%
filter(year >= 2015)
vw %>%
select(year, model) %>%
group_by(year, model) %>%
count() %>%
ungroup() %>%
complete(year, model, fill = list(n = 0)) %>%
mutate(faltante = ifelse(n == 0, "Sim", "Não")) %>%
ggplot(., aes(x = year, y = model, fill = faltante)) +
geom_tile(colour = "white") +
scale_x_continuous(breaks = seq(2015, 2020), labels = seq(2015, 2020)) +
labs(x = "Ano de Fabricação",
y = "Modelo do Carro",
fill = "Dado faltante?") +
scale_fill_viridis_d()
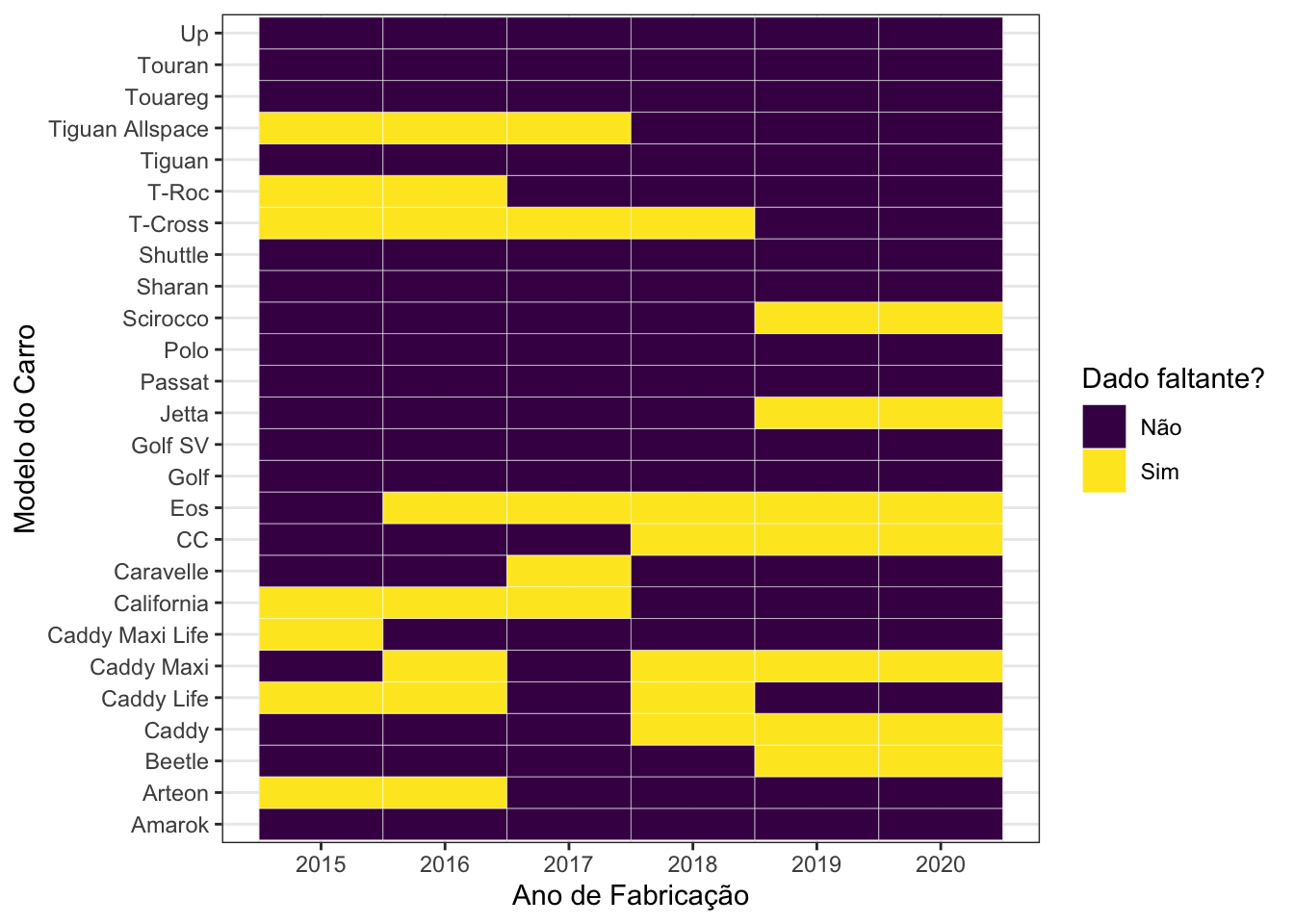
Com isso, apenas 25,64% das combinações estão faltando. Ainda assim, modelos como Eos, Caddy Maxi e Caddy Life parecem ter um comportamento não ideal, ainda com dados faltantes para muitos anos. Por isso, vou retirar todas as ocorrências deles do banco de dados.
vw <-
vw %>%
filter(model != "Eos" & model != "Caddy Maxi" & model != "Caddy Life")
vw %>%
select(year, model) %>%
group_by(year, model) %>%
count() %>%
ungroup() %>%
complete(year, model, fill = list(n = 0)) %>%
mutate(faltante = ifelse(n == 0, "Sim", "Não")) %>%
ggplot(., aes(x = year, y = model, fill = faltante)) +
geom_tile(colour = "white") +
scale_x_continuous(breaks = seq(2015, 2020), labels = seq(2015, 2020)) +
labs(x = "Ano de Fabricação",
y = "Modelo do Carro",
fill = "Dado faltante?") +
scale_fill_viridis_d()
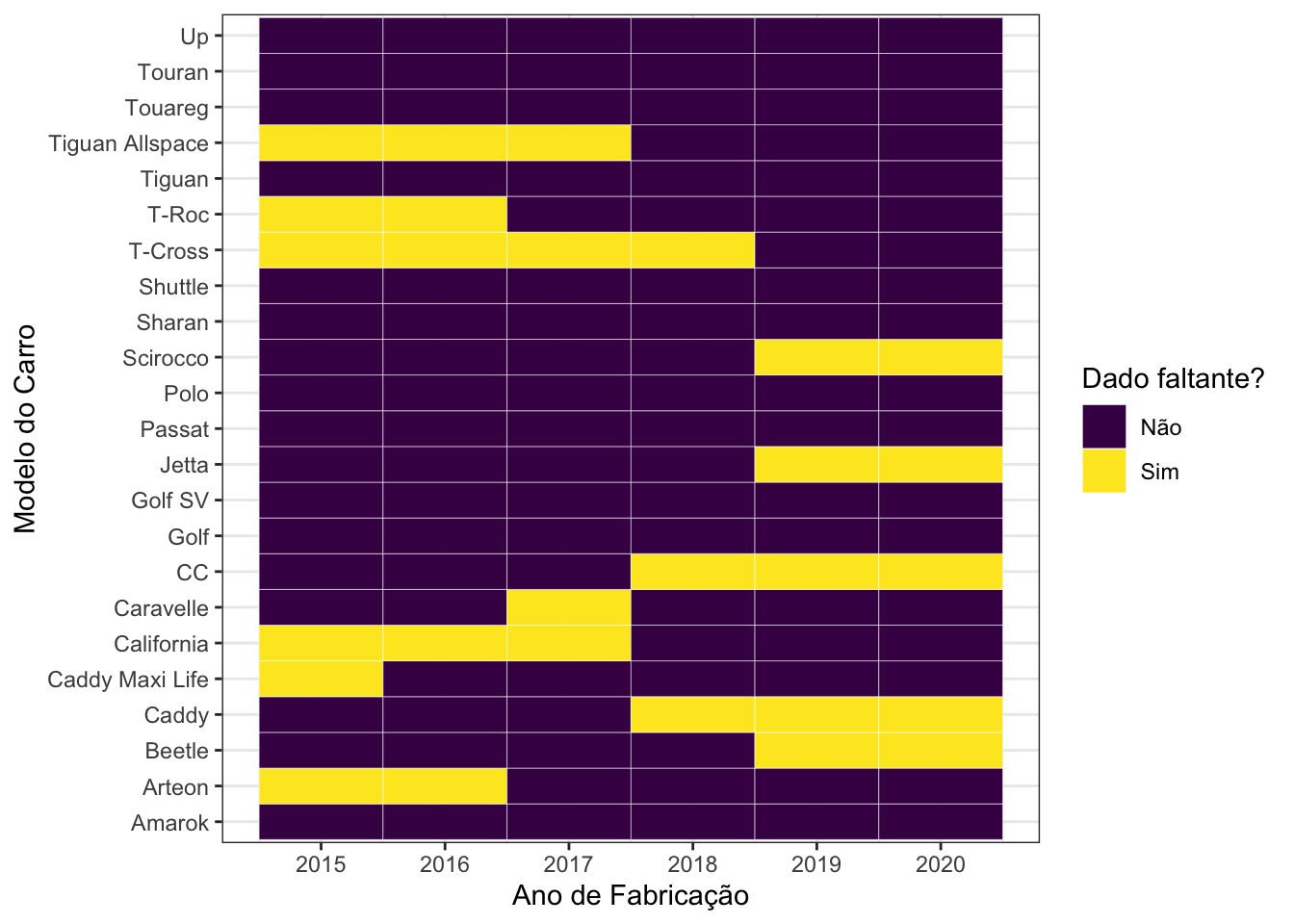
Agora sim, com apenas 20,29% de combinações entre anos e modelos de carros faltantes, podemos proceder com a análise. Além disso, continuamos com 13960 linhas no conjunto de dados a ser analisado, uma perda de apenas 7.9% em relação às 15157 linhas do conjunto de dados original.
Divisão dos Dados em Treinamento e Teste Link para o cabeçalho
Um post antigo deste blog, intitulado Tutorial: Como Fazer o Seu Primeiro Projeto de Data Science, discute a razão do porquê dividirmos os dados em treino e teste. Por este motivo, não irei justificar novamente a razão de termos que fazer algo nesta linha.
A partir de agora, utilizaremos o pacote tidymodels para tratar os dados antes das análises preditivas. Vamos dividir os dados em 75% para o treinamento e 25% para o teste.
# pacote necessario
library(tidymodels)
## ── Attaching packages ────────────────────────────────────── tidymodels 1.1.1 ──
## ✔ broom 1.0.5 ✔ rsample 1.2.0
## ✔ dials 1.2.1 ✔ tune 1.1.2
## ✔ infer 1.0.6 ✔ workflows 1.1.4
## ✔ modeldata 1.3.0 ✔ workflowsets 1.0.1
## ✔ parsnip 1.2.0 ✔ yardstick 1.3.0
## ✔ recipes 1.0.10
## ── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
## ✖ purrr::accumulate() masks foreach::accumulate()
## ✖ scales::discard() masks purrr::discard()
## ✖ dplyr::filter() masks stats::filter()
## ✖ recipes::fixed() masks stringr::fixed()
## ✖ dplyr::lag() masks stats::lag()
## ✖ yardstick::spec() masks readr::spec()
## ✖ recipes::step() masks stats::step()
## ✖ purrr::when() masks foreach::when()
## • Use suppressPackageStartupMessages() to eliminate package startup messages
# 75% dos dados como treino
set.seed(2410)
vw_split <- initial_split(vw, prop = .75)
# criar os conjuntos de dados de treino e teste
vw_treino <- training(vw_split)
vw_teste <- testing(vw_split)
Pré-Processamento das Variáveis Preditoras Link para o cabeçalho
Com os dados limpos e separados em treinamento e teste, o próximo passo para a análise é pré-processar as variáveis. São dois os passos que serão executados a partir de agora. O primeiro é a criação de variáveis dummy. Estas variáveis permitem que dados qualitativos sejam analisados em um contexto de regressão. Basicamente transformamos dados categóricos em numéricos.
O segundo passo é centrar e escalar as variáveis preditoras. Isto é, deixá-las todas com média 0 e desvio padrão 1. Este passo ajuda na convergência dos algoritmos que utilizaremos para nossa modelagem.
Ao final, teremos um objeto chamado vw_rec, que lembrará quais são os passos que utilizamos para preparar os dados para análise, de modo que as mesmas transformações possam ser aplicadas tanto no conjunto de treino quanto no conjunto de teste.
vw_rec <-
# regressao que serah aplicada aos dados
recipe(price ~ .,
data = vw_treino) %>%
# criacao das variaveis dummy
step_dummy(where(is.character)) %>%
# center/scale
step_center(where(is.numeric), -price) %>%
step_scale(where(is.numeric), -price) %>%
# funcao para aplicar a transformacao aos dados
prep()
Em seguida, a receita vw_rec é aplicada aos conjuntos de treino e teste.
# aplicar a transformacao aos dados
vw_treino_t <- juice(vw_rec)
# preparar o conjunto de teste
vw_teste_t <- bake(vw_rec,
new_data = vw_teste)
Com os dados preparados, é hora de partirmos para a modelagem propriamente dita.
Modelagem Link para o cabeçalho
O objetivo a partir de agora, com os dados preparados e transformados, é prever o preço dos carros em função das outras variáveis presentes no conjunto de dados. Duas abordagens serão utilizadas e comparadas. A primeira delas é a regressão linear. Em seguida, vou utilizar random forests. Para que ambas sejam comparáveis, vou utilizar o pacote tidymodels, de modo que as métricas sejam as mesmas para ambas as abordagens.
Regressão Linear Link para o cabeçalho
Embora tenhamos visto que os dados não possuem relações lineares entre si, vou começar com a regressão linear para ter uma baseline com a qual trabalhar.
O pacote tidymodels exige que definamos uma série de objetos intermediários para que o modelo possa ser ajutado aos dados. Mais informações sobre o significado de cada um deles podem ser encontradas em meu curso de Introdução à Modelagem de Big Data ou no próprio site do pacote tidymodels. Como o bjetivo deste texto é ser apenas uma aplicação das técnicas deste pacote, deixarei estas explicações para lá.
Na ordem, iremos criar o modelo a ser ajustado, o workflow para o ajuste, a definição da validação cruzada e ajustaremos o modelo definido com estas características.
# modelo
vw_lm <-
linear_reg() %>%
set_engine("lm")
vw_lm
## Linear Regression Model Specification (regression)
##
## Computational engine: lm
# criar workflow
vw_wflow <-
workflow() %>%
add_model(vw_lm) %>%
add_formula(price ~ .)
# definicao da validacao cruzada
set.seed(2410)
vw_treino_cv <- vfold_cv(vw_treino, v = 10)
vw_treino_cv
## # 10-fold cross-validation
## # A tibble: 10 × 2
## splits id
## <list> <chr>
## 1 <split [9423/1047]> Fold01
## 2 <split [9423/1047]> Fold02
## 3 <split [9423/1047]> Fold03
## 4 <split [9423/1047]> Fold04
## 5 <split [9423/1047]> Fold05
## 6 <split [9423/1047]> Fold06
## 7 <split [9423/1047]> Fold07
## 8 <split [9423/1047]> Fold08
## 9 <split [9423/1047]> Fold09
## 10 <split [9423/1047]> Fold10
# modelo ajustado com validacao cruzada
vw_lm_fit_cv <- fit_resamples(vw_wflow, vw_treino_cv)
vw_lm_fit_cv
## # Resampling results
## # 10-fold cross-validation
## # A tibble: 10 × 4
## splits id .metrics .notes
## <list> <chr> <list> <list>
## 1 <split [9423/1047]> Fold01 <tibble [2 × 4]> <tibble [0 × 3]>
## 2 <split [9423/1047]> Fold02 <tibble [2 × 4]> <tibble [0 × 3]>
## 3 <split [9423/1047]> Fold03 <tibble [2 × 4]> <tibble [0 × 3]>
## 4 <split [9423/1047]> Fold04 <tibble [2 × 4]> <tibble [0 × 3]>
## 5 <split [9423/1047]> Fold05 <tibble [2 × 4]> <tibble [0 × 3]>
## 6 <split [9423/1047]> Fold06 <tibble [2 × 4]> <tibble [0 × 3]>
## 7 <split [9423/1047]> Fold07 <tibble [2 × 4]> <tibble [0 × 3]>
## 8 <split [9423/1047]> Fold08 <tibble [2 × 4]> <tibble [0 × 3]>
## 9 <split [9423/1047]> Fold09 <tibble [2 × 4]> <tibble [0 × 3]>
## 10 <split [9423/1047]> Fold10 <tibble [2 × 4]> <tibble [0 × 3]>
# resultados
collect_metrics(vw_lm_fit_cv)
## # A tibble: 2 × 6
## .metric .estimator mean n std_err .config
## <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 rmse standard 2505. 10 30.7 Preprocessor1_Model1
## 2 rsq standard 0.893 10 0.00289 Preprocessor1_Model1
Como as métricas da validação cruzada estão satisfatórias, iremos ajustar o modelo no conjunto de treino completo para, em seguida, verificar o resultado obtido no conjunto de teste.
# ajuste do modelo no conjunto de treino completo
vw_lm_fit_treino <- fit(vw_wflow, vw_treino)
# resultados no conjunto de teste
resultado <-
vw_teste %>%
bind_cols(predict(vw_lm_fit_treino, vw_teste) %>%
rename(predicao_lm = .pred))
# resultado final
metrics(resultado,
truth = price,
estimate = predicao_lm)
## # A tibble: 3 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 rmse standard 2413.
## 2 rsq standard 0.893
## 3 mae standard 1785.
Comparando as métricas obtidas no conjunto de treino com o conjunto de teste, é possível dizer que não há sobreajuste, dado que os resultados estão muito próximos.
Ao comparar os valores preditos pelo modelo com os que estavam no conjunto teste, obtemos o gráfico a seguir.
# grafico final
ggplot(resultado, aes(x = price, y = predicao_lm)) +
geom_point() +
labs(x = "Valores Observados", y = "Valores Preditos") +
geom_abline(intercept = 0, slope = 1) +
coord_fixed()
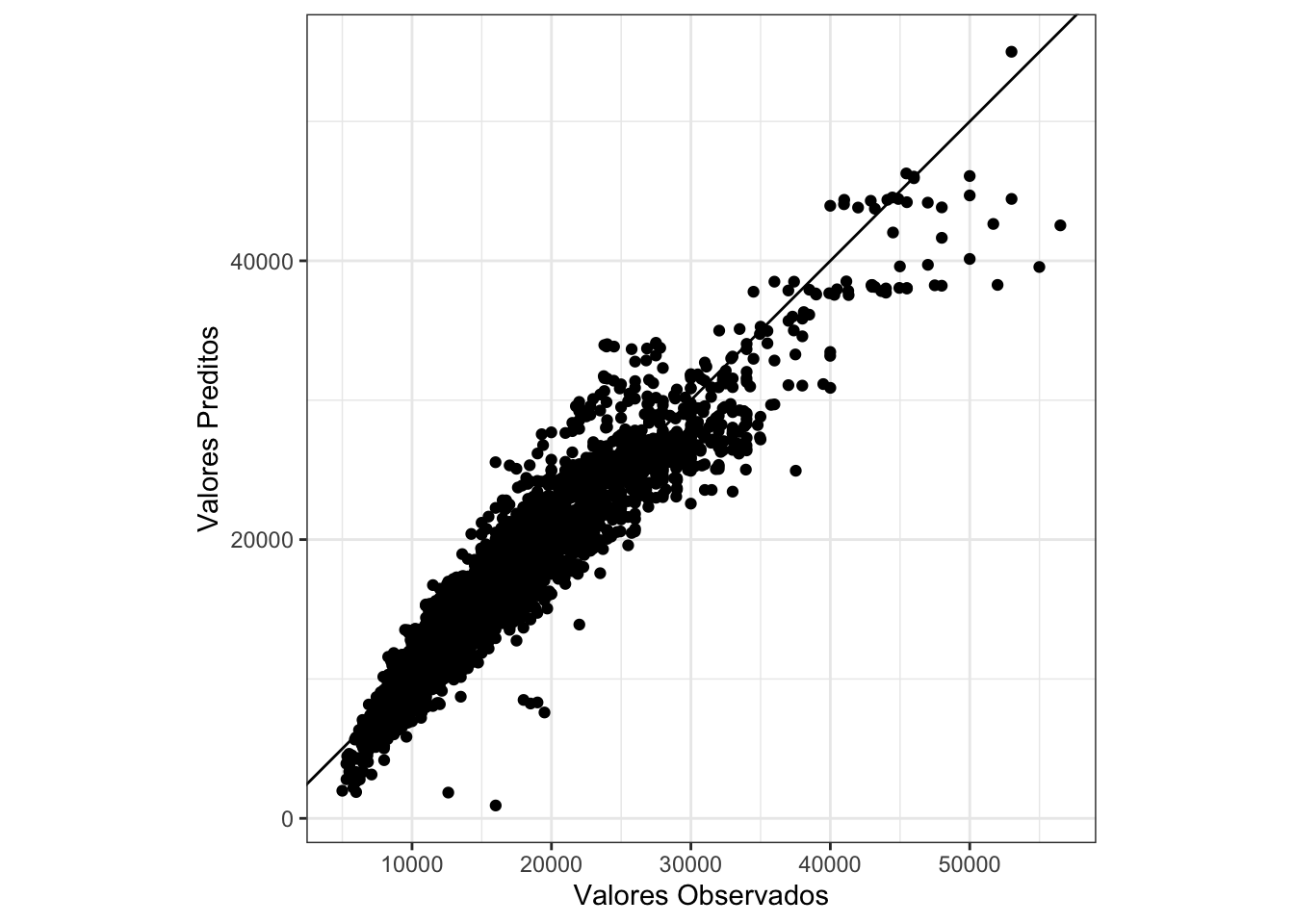
Caso a nossa predição tivesse ficado perfeita, o gráfico acima deveria se comportar como uma reta. Como é possível perceber, o comportamento não está como o ideal. Por isso, tentaremos uma nova abordagem para os dados. Iremos utilizar um algoritmo muito famoso para isso, chamado random forests.
Random Forests Link para o cabeçalho
Uma grande vantagem das random forests sobre a regressão linear é a inexistência de uam exigência a respeito da linearidade dos dados. Com isso, torna-se algo muito mais versátil do que um método que só pode lidar com dados lineares.
Como estamos utilizando o pacote tidymodels, é possível reaproveitar grande parte do código utilizado para ajustar a regressão linear. As funções a serem utilizadas são rigorosamente as mesmas, com pequenas mudanças em seus argumentos.
Entretanto, será necessário adicionar algumas funções extras, a fim de realizar o tuning dos parâmetros para o modelo ajustado, a fim de minimizar o erro de predição do preço dos automóveis.
# definicao do tuning
vw_rf_tune <-
rand_forest(
mtry = tune(),
trees = 1000,
min_n = tune()
) %>%
set_mode("regression") %>%
set_engine("ranger", importance = "impurity")
# grid de procura
vw_rf_grid <- grid_regular(mtry(range(1, 8)),
min_n(range(10, 50)))
vw_rf_grid
## # A tibble: 9 × 2
## mtry min_n
## <int> <int>
## 1 1 10
## 2 4 10
## 3 8 10
## 4 1 30
## 5 4 30
## 6 8 30
## 7 1 50
## 8 4 50
## 9 8 50
# workflow
vw_rf_tune_wflow <-
workflow() %>%
add_model(vw_rf_tune) %>%
add_formula(price ~ .)
# definicao da validacao cruzada
set.seed(2410)
vw_treino_cv <- vfold_cv(vw_treino_t, v = 10)
# avaliacao do modelo
vw_rf_fit_tune <-
vw_rf_tune_wflow %>%
tune_grid(
resamples = vw_treino_cv,
grid = vw_rf_grid
)
# resultados
collect_metrics(vw_rf_fit_tune)
## # A tibble: 18 × 8
## mtry min_n .metric .estimator mean n std_err .config
## <int> <int> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 1 10 rmse standard 2408. 10 41.1 Preprocessor1_Model1
## 2 1 10 rsq standard 0.921 10 0.00232 Preprocessor1_Model1
## 3 4 10 rmse standard 1645. 10 34.3 Preprocessor1_Model2
## 4 4 10 rsq standard 0.954 10 0.00183 Preprocessor1_Model2
## 5 8 10 rmse standard 1703. 10 32.1 Preprocessor1_Model3
## 6 8 10 rsq standard 0.950 10 0.00175 Preprocessor1_Model3
## 7 1 30 rmse standard 2448. 10 39.9 Preprocessor1_Model4
## 8 1 30 rsq standard 0.918 10 0.00239 Preprocessor1_Model4
## 9 4 30 rmse standard 1692. 10 34.6 Preprocessor1_Model5
## 10 4 30 rsq standard 0.951 10 0.00188 Preprocessor1_Model5
## 11 8 30 rmse standard 1723. 10 32.1 Preprocessor1_Model6
## 12 8 30 rsq standard 0.949 10 0.00174 Preprocessor1_Model6
## 13 1 50 rmse standard 2503. 10 47.6 Preprocessor1_Model7
## 14 1 50 rsq standard 0.914 10 0.00273 Preprocessor1_Model7
## 15 4 50 rmse standard 1753. 10 36.0 Preprocessor1_Model8
## 16 4 50 rsq standard 0.948 10 0.00195 Preprocessor1_Model8
## 17 8 50 rmse standard 1781. 10 33.7 Preprocessor1_Model9
## 18 8 50 rsq standard 0.946 10 0.00183 Preprocessor1_Model9
Novamente, as métricas da validação cruzada estão satisfatórias. Agora iremos verificar o desempenho dos hiperparâmetros do modelo, a fim de verificar se foram encontrados pontos de mínimo para o RMSE em cada um deles.
vw_rf_fit_tune %>%
collect_metrics() %>%
mutate(min_n = factor(min_n)) %>%
ggplot(., aes(x = mtry, y = mean, colour = min_n, group = min_n)) +
geom_line() +
geom_point() +
facet_grid(.metric ~ ., scales = "free") +
scale_x_continuous(breaks = seq(1, 9, 2)) +
scale_colour_viridis_d()
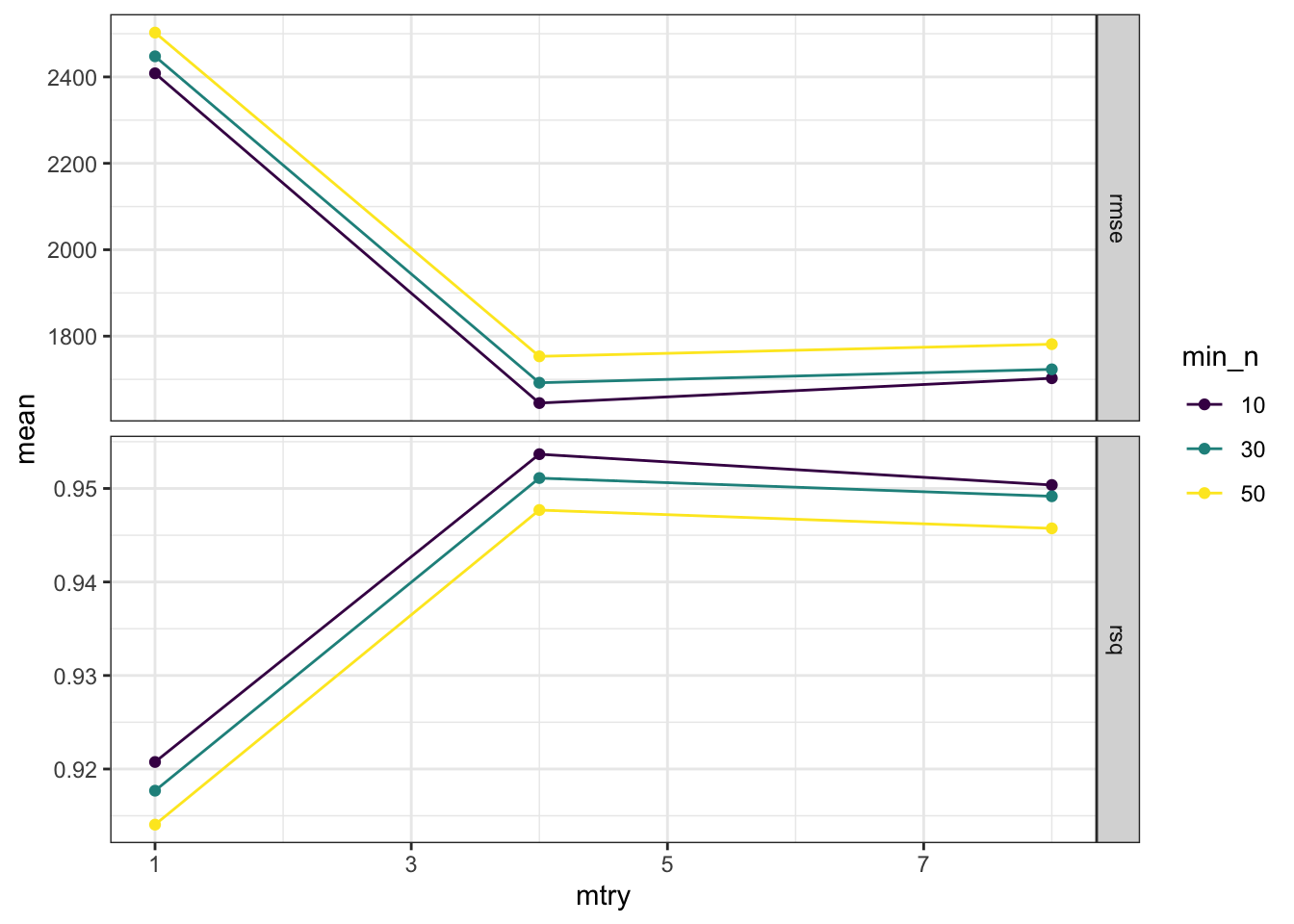
Tudo certo de acordo com o gráfico acima. Conseguimos obter o mínimo de RMSE (ou seja, o menor erro possível) e o máximo de \(R^2\) (nosso pseudo coeficiente de determinação) de maneira global. Os resultados apresentados no gráfico poderiam ser refinados se fosse criado um objeto vw_rf_tune com mais pontos para mtry, min_n ou até mesmo trees. Entretanto, isso faria com que mais modelos fossem gerados, o que elevaria o tempo de execução do ajuste dos modelos considerados.
Como foram gerados vários modelos diferentes a partir dos hiperparâmetros definidos, é preciso agora encontrar aqueles modelos que geraram os melhores resultados. Após, iremos ajustar no conjunto de treino completo aquele modelo cujos hiperparâmetros geraram o menor RMSE.
# melhores modelos
vw_rf_fit_tune %>%
show_best("rmse")
## # A tibble: 5 × 8
## mtry min_n .metric .estimator mean n std_err .config
## <int> <int> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 4 10 rmse standard 1645. 10 34.3 Preprocessor1_Model2
## 2 4 30 rmse standard 1692. 10 34.6 Preprocessor1_Model5
## 3 8 10 rmse standard 1703. 10 32.1 Preprocessor1_Model3
## 4 8 30 rmse standard 1723. 10 32.1 Preprocessor1_Model6
## 5 4 50 rmse standard 1753. 10 36.0 Preprocessor1_Model8
# melhor modelo
vw_rf_best <-
vw_rf_fit_tune %>%
select_best("rmse")
vw_rf_final <-
vw_rf_tune_wflow %>%
finalize_workflow(vw_rf_best)
vw_rf_final <- fit(vw_rf_final,
vw_treino_t)
vw_rf_final
## ══ Workflow [trained] ══════════════════════════════════════════════════════════
## Preprocessor: Formula
## Model: rand_forest()
##
## ── Preprocessor ────────────────────────────────────────────────────────────────
## price ~ .
##
## ── Model ───────────────────────────────────────────────────────────────────────
## Ranger result
##
## Call:
## ranger::ranger(x = maybe_data_frame(x), y = y, mtry = min_cols(~4L, x), num.trees = ~1000, min.node.size = min_rows(~10L, x), importance = ~"impurity", num.threads = 1, verbose = FALSE, seed = sample.int(10^5, 1))
##
## Type: Regression
## Number of trees: 1000
## Sample size: 10470
## Number of independent variables: 8
## Mtry: 4
## Target node size: 10
## Variable importance mode: impurity
## Splitrule: variance
## OOB prediction error (MSE): 2658260
## R squared (OOB): 0.9545377
Agora que o melhor modelo foi encontrado, podemos verificar os resultados obtidos por ele no conjunto de teste.
# resultados no conjunto de teste
resultado_rf <-
vw_teste_t %>%
bind_cols(predict(vw_rf_final, vw_teste_t) %>%
rename(predicao_rf = .pred))
metrics(resultado_rf,
truth = price,
estimate = predicao_rf)
## # A tibble: 3 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 rmse standard 1513.
## 2 rsq standard 0.958
## 3 mae standard 1006.
metrics(resultado,
truth = price,
estimate = predicao_lm)
## # A tibble: 3 × 3
## .metric .estimator .estimate
## <chr> <chr> <dbl>
## 1 rmse standard 2413.
## 2 rsq standard 0.893
## 3 mae standard 1785.
Como podemos ver, o RMSE no conjunto de teste para o random forest ficou em 1514 (1630 no conjunto de treino, indicando que não houve sobreajuste), bem abaixo dos 2413 obtidos pela regressão linear. O mesmo vale para o \(R^2\) do random forest, bem acima daquele obtido pela regressão linear.
Ao comparar graficamente os valores preditos pelo modelo com aqueles disponíveis no conjunto de teste, temos um resultado muito bom e, como era de se supor, bastante superior ao da regressão linear. A variância destes dados está muito menor, indicando que o ajuste foi muito bem feito.
# grafico final
ggplot(resultado_rf, aes(x = price, y = predicao_rf)) +
geom_point() +
labs(x = "Valores Observados", y = "Valores Preditos") +
geom_abline(intercept = 0, slope = 1) +
coord_fixed()
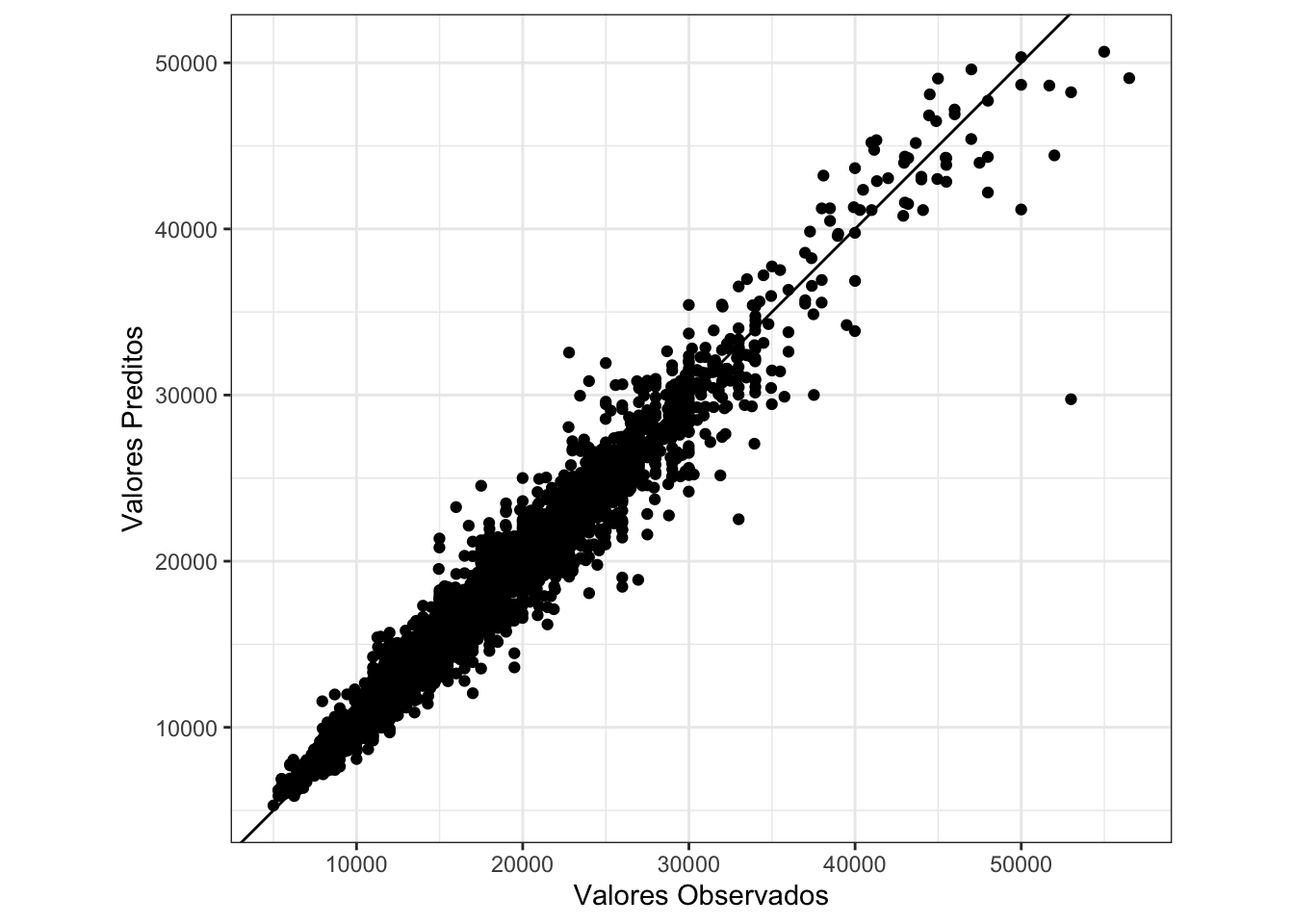
Por fim, podemos encontrar as variáveis mais importantes para a determinação do preço dos automóveis.
# importancia das variaveis
library(vip)
##
## Attaching package: 'vip'
## The following object is masked from 'package:utils':
##
## vi
vw_rf_final %>%
extract_fit_parsnip() %>%
vip(scale = TRUE)
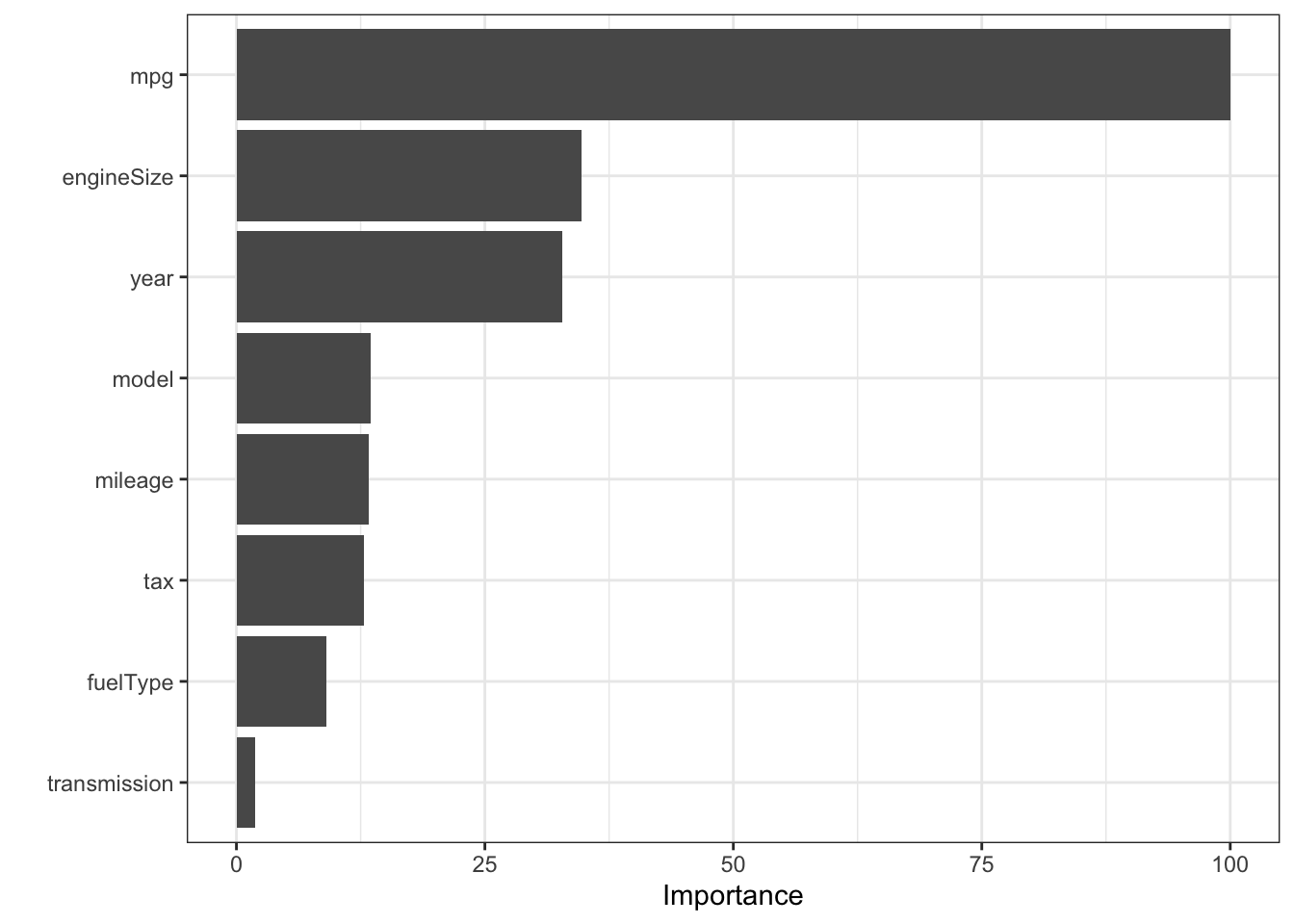
A variável que melhor determina o preço dos automóveis fabricados pela Volkswagen no mercado de usados no Reino Unido é o consumo, seguido de longe pelo tamanho do motor, ano de fabricação, modelo do carro e assim por diante. O tipo de câmbio é o que menos importa neste mercado.
Conclusões Link para o cabeçalho
Utilizar o tidymodels para ajustar modelos aos nossos dados é bastante simples. A grande vantagem é poder usar um conjunto padrão de funções que podem ser reaproveitadas pelos mais diferentes métodos de modelagem.
Fica a cargo do leitor ajustar modelos para os outros fabricantes de automóveis disponíveis neste conjunto de dados.
Todos os arquivos utilizados podem ser baixados no github.